| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- 파이토치
- Self-supervised
- Python
- pytorch
- Convolution
- opencv
- 머신러닝
- 인공지능
- Paper Review
- 프로그래머스
- 파이썬
- ViT
- programmers
- 코딩테스트
- 논문 리뷰
- 딥러닝
- 논문
- Ai
- 논문구현
- 코드구현
- Segmentation
- transformer
- 논문리뷰
- Computer Vision
- Semantic Segmentation
- optimizer
- 옵티마이저
- cnn
- object detection
- 알고리즘
- Today
- Total
Attention please
[딥러닝] LeCun / Xavier / He 초기값 설정 - 표현력 제한, vanishing gradient문제 보완 본문
[딥러닝] LeCun / Xavier / He 초기값 설정 - 표현력 제한, vanishing gradient문제 보완
Seongmin.C 2022. 10. 1. 12:162022.09.30 - [딥러닝] - 옵티마이저(optimizer) - Adam
옵티마이저(optimizer) - Adam
2022.09.30 - [딥러닝] - 옵티마이저(optimizer) - RMSProp 옵티마이저(optimizer) - RMSProp 2022.09.30 - [딥러닝] - 옵티마이저(optimizer) - AdaGrad 옵티마이저(optimizer) - AdaGrad 2022.09.30 - [딥러닝]..
smcho1201.tistory.com
지금까지 optimizer 기법들에 대해 살펴보았습니다.
이번 글에서는 학습을 시키기 전
가중치값들을 어떻게 초기화해야 하는지에 대해 살펴보겠습니다.
가중치 초기값 설정
왜 가중치를 초기화 하는 것이 중요할까요?
사실 많은 사람들이 앞서 설명드렸던 optimizer나 모델의 구성에 대해서만 관심을 두고
가중치에 대해서는 관심을 두지 않는 경우가 많습니다.
그렇다면 가중치를 초기화 하는 것이 왜 중요한지 알아보겠습니다.
보통 가중치를 초기화 할 때는 평균과 표준편차를 정해두고
랜덤으로 숫자들을 부여합니다.
첫 번째로 평균이 0, 표준편차가 1인 정규분포로
가중치를 초기화 하면

Vanishing Gradient 문제가 생기게 됩니다.
그렇다면 이번에는 가중치를
평균이 0, 표준편차를 0.01인 정규분포로 초기화하면

표현력이 제한되는 문제가 생깁니다.
표준편차가 0.01 즉, 너무 작게 주어지면 가중치에 주어지는 데이터들이 거의 비슷해집니다.
즉 가중치 matrix를 이루는 원소들의 값들이 거의 0 혹은 그 근처의 값들이 주어지게 됩니다.
표현력 제한
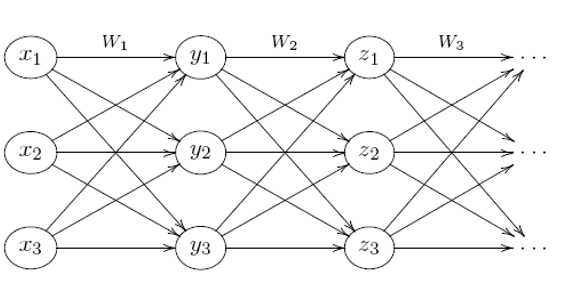
한번 위와 같은 그림의 신경망이 있다고 생각을 하고
첫번째 가중치 행렬의 각 행이 동일하고,
두번째 부터는 각 층마다 가중치 행렬의 모든 원소가 동일합니다.
$$ \begin{align*} W_{1} = \begin{pmatrix} w_{1} & w_{1} & w_{1} \\ w_{2} & w_{2} & w_{2} \\ w_{3} & w_{3} & w_{3} \\ \end{pmatrix} \\ \\ W_{2} = \begin{pmatrix} w^{'} & w^{'} & w^{'} \\ w^{'} & w^{'} & w^{'} \\ w^{'} & w^{'} & w^{'} \\ \end{pmatrix} \\ \\ W_{3} = \begin{pmatrix} w^{''} & w^{''} & w^{''} \\ w^{''} & w^{''} & w^{''} \\ w^{''} & w^{''} & w^{''} \\ \end{pmatrix}\end{align*}$$

그러면 아까 위의 신경망이 결국 위의 그림과 같이
1층 부터 뉴런의 개수가 모두 1개인 신경망과 본질적으로 같아지게 됩니다.
가중치를 살펴보면
$$ \begin{align*} W1 = \begin{pmatrix} w_{1} \\ w_{2} \\ w_{3} \end{pmatrix}\\ \\ W2 = (3w^{'}) \\ \\ W3 = (3w^{''}) \end{align*}$$
위의 가중치 행렬과 위의 식이 결국 본질적으로 같다는 것을 알 수 있습니다.
왜 이런식으로 신경망이 단순해지는지 수학적으로 확인해보겠습니다.
$$ \begin{align*} sigmoid([x1\; x2\; x3] \begin{bmatrix} w_{1} & w_{1} & w_{1} \\ w_{2} & w_{2} & w_{2} \\ w_{3} & w_{3} & w_{3} \\ \end{bmatrix}) \end{align*} $$
$$ \begin{align*} = sigmoid(\begin{bmatrix} \sum_{i=1}^{3} w_{i}x_{i}, \; \sum_{i=1}^{3} w_{i}x_{i}, \; \sum_{i=1}^{3} w_{i}x_{i}\end{bmatrix}) = \begin{bmatrix} sigmoid(\sum_{i=1}^{3} w_{i} x_{i}), \; sigmoid(\sum_{i=1}^{3} w_{i} x_{i}), \; sigmoid(\sum_{i=1}^{3} w_{i} x_{i}) \end{bmatrix} \end{align*}$$
즉 학습을 진행해도 각 가중치 행렬의 원소들은 바뀌지만
각 원소들은 모두 동일하게 됩니다.
처음 뉴럴 네트워크를 뉴런이
$$ 1000 \rightarrow \; 1000 \; \rightarrow \; \cdot \cdot \cdot$$
으로 가는 아주 복잡한 신경망이였다 해도 실질적으로는
$$ 1000 \rightarrow \; 1 \; \rightarrow \; 1 \; \rightarrow \; \cdot \cdot \cdot$$
와 같은 아주 단순한 신경망과 같다는 것을 의미하게 됩니다.
(뉴럴 네트워크를 통해 학습을 시키게 되면 데이터의 정보들이 weight와 bias에 담기게 되는데
위와 같이 단순화가 되면 데이터를 담을 수 있는 슬롯이 너무 적어지게 되어 문제가 생김)
즉, 가중치를 평균 0, 표준편차 0.01로 잡게 되면
데이터의 정보를 담을 수 있는 슬롯의 개수가 겉보기에는 많아 보일 수 있어도
실질적으로는 굉장히 적다는 것입니다.
"표준편차를 너무 작게 잡으면 안된다"
Vanishing Gradient Problem
그러면 가중치를 평균 0, 표준편차 1인 정규분포로 초기화 하였을 때
vanishing gradient 문제가 왜 생기는 걸까?

vanishing gradient 는 위의 사진과 같이 역전파를 사용하여 학습을 할 때 생기는 문제입니다.
계속 학습을 하며 밑의 층으로 내려가게 되면 학습이 거의 이루어 지지 않게 됩니다.
그렇다면 왜 학습이 이루어지지 않을까?
아까 위에서 가중치를 초기화할 때
평균을 0, 표준편차 1인 정규분포로 초기화를 하게 되면
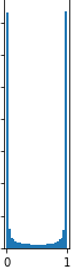
와 같이 sigmoid 함수 값이 0과 1에 몰려있게 됩니다.
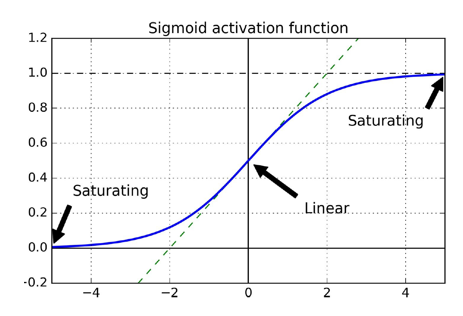
이런상황이 왜 문제가 될까요?
역전파를 할 때 우리는 미분을 하게 됩니다.
즉 sigmoid 값이 0과 1인 부분에서 미분을 하여
optimizer기법을 사용하며 산을 내려가게 되는데
sigmoid함수 특성상 y축의 값중 1과 0부분의 함수 기울기가 거의 0에 가깝습니다.
즉 미분을 해도 0에 근사하는 값이 나온다는 의미입니다.
결국 학습이 적게 이루어지게 되는 결과가 나오게 됩니다.
표준편차를 너무 작게 잡으면
뉴럴 네트워크를 복잡하게 설계하였다고 해도
실질적으로는 굉장히 단순한 뉴럴 네트워크가 본질적으로 같아진다.
데이터의 정보를 담을 수 있는 슬롯 즉 parameter의 수가 너무 적어져
표현력의 문제가 생긴다.
표준편차를 너무 크게 잡으면
역전파를 따라서 밑에 층으로 계속 내려가면서 점점 사라져가게 된다.
위의 층은 학습이 어느정도 되지만
밑에 층은 학습이 거의 안되기 때문에 층을 깊게 쌓는 이유가 사라지게 된다.
결국 vanishing gradient 문제가 생기게 된다.
우리는 이러한 문제를 해결하기 위해
학습 시작 전 weight를 랜덤하게 설정할 때
표준편차를 너무 크지도 작지도 않게 적절한 값을 찾아 설정해야 합니다.
물론 저희가 직접 찾을 필요는 없습니다.
이미 만들어진 공식이 있으니까요.
먼저 보여드릴 공식은 LeCun 초기값과 Xavier 초기값입니다.
$$\begin{align*} LeCun\; initialization : W \sim N(0, \frac {1} {n_{in}}) \end{align*}$$
$$\begin{align*} Xavier\; initialization : W \sim N(0, \frac {2} {n_{in} + n_{out}}) \end{align*}$$
$$n_{in} : num\; of\; input\; neurons,\quad n_{out} : num\; of\; output\; neurons$$
(참고자료인 "밑바닥부터 시작하는 딥러닝" 에서는
LeCun, Xavier 초기값을 위와 같이 정의했지만,
일반적으로는 LeCun 초기값은 쓰이지 않고
LeCun 초기값의 정의를 Xavier 초기값으로 사용합니다.)
Xavier 초기값은 n(in)과 n(out)의 평균의 역수라고 생각하시면 됩니다.
$$\frac {1} {\frac {n_{in} + n_{out}} {2}} = \frac {2} {n_{in} + n_{out}}$$
가중치 초기값으로 LeCun 초기값을 주게 되면

각층의 활성화 값 분포가 위와 같이 배치된 것을 볼 수 있습니다.
확실히 아까와는 다르게 고르게 종 모양으로 분포되어 있는 것을 알 수 있습니다.
지금까지 설명드린 초기값들은 활성화 함수를 sigmoid로 잡았을 때 설정하게 됩니다.
다음으로는 활성화 함수를 ReLU로 잡았을 때 사용하게 되는 He초기값에 대해 보여드리겠습니다.
$$ He\; initialization : W \sim N(0, \frac {2} {n_{in}})$$
위의 수식은 He 초기값에 대한 수식입니다.
하지만
왜 ReLU를 활성화 함수로 선택할 때 He초기값을 사용해야 될까요?

위의 사진은 LeCun 초기값을 사용하였을 때 가중치 값들의 분포입니다.
보시다시피 그리 고른 형태가 아니라는 것을 볼 수 있습니다.
그렇다면 He 초기값은 어떨까요?

아까 보여드렸던 LeCun 초기값을 사용했을 때에 비해
가중치들의 분포가 상당히 고르게 퍼져있는 것을 볼 수 있습니다.
이러한 이유로 활성화 함수를 어떤 것을 사용하는 가에 따라
사용되는 초기값의 종류가 달라지게 됩니다.
'딥러닝 > DNN' 카테고리의 다른 글
| [딥러닝] Regularization(Weight Decay, Dropout) - overfitting(과적합) 억제 (2) | 2022.10.30 |
|---|---|
| [딥러닝] Batch Normalization (배치정규화) (0) | 2022.10.27 |
| [딥러닝] 옵티마이저(optimizer) - Adam (0) | 2022.09.30 |
| [딥러닝] 옵티마이저(optimizer) - RMSProp (0) | 2022.09.30 |
| [딥러닝] 옵티마이저(optimizer) - AdaGrad (0) | 2022.09.30 |




