| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- ViT
- Self-supervised
- 코딩테스트
- object detection
- Python
- Segmentation
- Ai
- 논문
- pytorch
- 논문리뷰
- 옵티마이저
- Paper Review
- 파이토치
- 코드구현
- 딥러닝
- 논문 리뷰
- 프로그래머스
- 파이썬
- Semantic Segmentation
- Convolution
- cnn
- 알고리즘
- optimizer
- 머신러닝
- programmers
- 논문구현
- transformer
- 인공지능
- opencv
- Computer Vision
- Today
- Total
Attention please
[딥러닝] Regularization(Weight Decay, Dropout) - overfitting(과적합) 억제 본문
[딥러닝] Regularization(Weight Decay, Dropout) - overfitting(과적합) 억제
Seongmin.C 2022. 10. 30. 14:122022.10.27 - [딥러닝] - Batch Normalization (배치정규화)
Batch Normalization (배치정규화)
2022.10.01 - [딥러닝] - LeCun / Xavier / He 초기값 설정 - 표현력 제한, vanishing gradient문제 보완 LeCun / Xavier / He 초기값 설정 - 표현력 제한, vanishing gradient문제 보완 2022.09.30 - [딥러닝] -..
smcho1201.tistory.com
이전 글에서는 Batch Normalization층에 대해 알아보았습니다.
이번 글에서는 Batch Norm층의 장점 중 하나인 overfitting이란 무엇이고,
overfitting을 억제하기 위한 다른 2가지 방법을 알아보겠습니다.
Overfitting
Overfitting, 번역하면 과적합입니다.
말 그대로 train data에 너무 최적화되어 weight값이 업데이트되어,
train data에 대해서는 좋은 성능을 보이지만
새로운 데이터에 대해서는 성능이 오히려 떨어지게 되는 현상을 의미합니다.
Overfitting은 보통 모델의 파라미터 수에 비해
train data 수가 적을 때 발생하게 됩니다.
이 문제는 현재까지도 완벽히 해결할 수 있는 방법은 나오지 않았습니다.
다만 이를 억제하기 위해서 다양한 방법들이 있는데
간단한 방법으로는 train data수가 적음으로 발생하는 문제이므로
반대로 train data의 수를 늘려주거나, 모델의 파라미터 수를 줄여주는 방법이 있습니다.
또 Overfitting이 되기 전에 학습을 멈추어 가장 최상의 성능을 가지는
weight값을 저장하는 방법이 있으며, 이를 Early Stopping이라 합니다.

하지만 train data를 Overfitting이 억제될정도로 구하기란 쉬운일이 아니며,
기본적으로 모델의 층이 깊어질 수록 성능이 좋아지기에
모델의 단순화 역시 좋은 방법은 아닙니다.
그렇게 나온 Overfitting을 억제하기 위해 다양한 방법론들이 주장되었고,
그중 Regularization(규제)에 대해 알아보겠습니다.
Regularization
overfitting은 모델이 데이터에 대해 너무 과적합되어 발생하는 문제입니다.
즉, 새로운 데이터에 대해서 적합하게 만들기 위해
학습하는 과정에서 데이터에 대해 덜 적합하게 하기 위해 규제를 넣어주는 것입니다.
즉 regularization을 함으로써 overfitting을 어느정도 막을 수 있으며,
이번 글에서는 regularization의 방법인 Weight Decay와 Dropout을 소개하겠습니다.
(overfitting을 막을 수 있는 완벽한 방법은 아직 존재하지 않는다)
Weight Decay
regularization의 방법중 하나인 weight decay 에는 두가지 방법이 존재합니다.
"L(1) - regularization" 과 "L(2) - regularization" 인데,
두 규제 모두 기존의 손실함수에 패널티를 더해 새로운 손실함수를 만들어
정보를 잃게 하여 overfitting을 방지합니다.
L(1)-regularization : 새로운 손실함수 = 기존 손실함수 + λ×(가중치의 절대값의 합)
L(1) 규제는 모든 가중치를 적게 낮추어 작은 가중치들을 사라지게 합니다.
L(2)-regularization : 새로운 손실함수 = 기존 손실함수 + 1/2×λ×(가중치의 제곱의 합)
L(2) 규제는 큰 가중치는 크게 낮추고, 작은 가중치는 적게 낮춥니다.
(λ는 가중치 감소 계수로
클수록 패널티의 역할이 커지고, 정보를 더 많이 잃게 한다)
Optimizer가 패널티를 더한 새로운 손실함수를 낮추는 것은
기존의 손실함수와 패널티 둘 모두 낮추는 것입니다.
기존의 손실함수를 낮추는 것은 가중치가 데이터에 fitting되어가는 것을 의미하고,
패널티를 낮추는 것은 가중치 모두를 0으로 만들어 정보를 잃게 하는 것을 의미합니다.
Dropout
regularization을 위한 방법인 Dropout은
뉴런을 무작위로 선택해 삭제하여 신호전달을 차단하는 방식으로 진행됩니다.
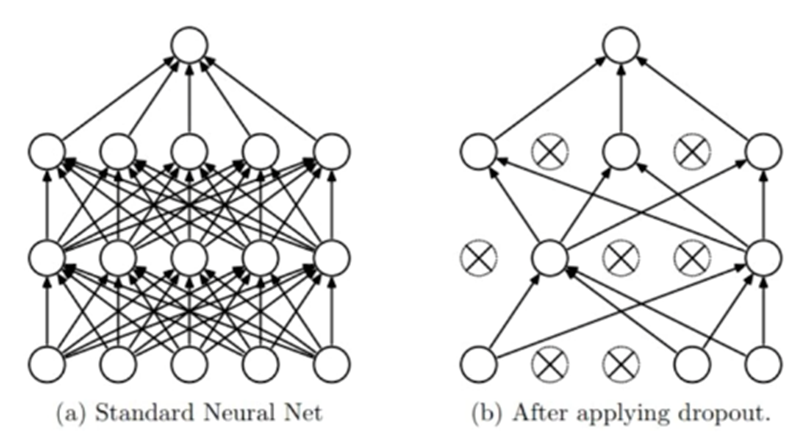
왼쪽 (a)가 Dropout을 적용하기 전의 신경망 모습입니다.
Dropout을 적용하게 되면 사람이 정해준 일정 비율로
랜덤하게 뉴런을 죽이고, 이를 매 학습할때마다 반복합니다.
물론 Dropout은 train할 때 overfitting을 방지하기 위해 존재하는 층이며,
test를 할 때는 뉴런들을 랜덤하게 죽이지 않습니다.
'딥러닝 > DNN' 카테고리의 다른 글
| [딥러닝] Batch Normalization (배치정규화) (0) | 2022.10.27 |
|---|---|
| [딥러닝] LeCun / Xavier / He 초기값 설정 - 표현력 제한, vanishing gradient문제 보완 (4) | 2022.10.01 |
| [딥러닝] 옵티마이저(optimizer) - Adam (0) | 2022.09.30 |
| [딥러닝] 옵티마이저(optimizer) - RMSProp (0) | 2022.09.30 |
| [딥러닝] 옵티마이저(optimizer) - AdaGrad (0) | 2022.09.30 |




