| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 파이토치
- 머신러닝
- optimizer
- transformer
- Ai
- 코딩테스트
- opencv
- ViT
- object detection
- 논문리뷰
- 강화학습
- Python
- cnn
- Computer Vision
- 파이썬
- Semantic Segmentation
- 프로그래머스
- 옵티마이저
- pytorch
- 코드구현
- Convolution
- 딥러닝
- Self-supervised
- 논문구현
- 논문 리뷰
- programmers
- 알고리즘
- Segmentation
- 논문
- 인공지능
- Today
- Total
Attention please
[딥러닝] 옵티마이저(optimizer) - Adam 본문
2022.09.30 - [딥러닝] - 옵티마이저(optimizer) - RMSProp
옵티마이저(optimizer) - RMSProp
2022.09.30 - [딥러닝] - 옵티마이저(optimizer) - AdaGrad 옵티마이저(optimizer) - AdaGrad 2022.09.30 - [딥러닝] - 옵티마이저(optimizer) - NAG 옵티마이저(optimizer) - NAG 2022.09.30 - [딥러닝] - 옵티마..
smcho1201.tistory.com
지난 글에서는 RMSProp기법에 대해 알아보았습니다.
이번 글에서는 가장 많이 쓰인다는 Adam에 대해 알아보겠습니다.
Adam
지금까지 알아본 optimizer기법들은
가장 기본인 SGD기법의 문제점들을 보완하기 위해 만들어졌었다.
Momentum, NAG, AdaGrad, RMSProp
이렇게 총 4가지의 optimizer기법들을 살펴보았습니다.
이번에 소개할 Adam은 지금까지의 optimizer들의 장점들을 합쳐놓은 것입니다.
정확히는 Momentum과 RMSProp 두가지 방식을 합쳐놓았습니다.
아무래도 각 기법들의 장점들만 모아논 기법이다 보니
Adam은 현재 가장 많이 쓰이는 optimizer입니다.
수식
위에서 말했던 것처럼 Adam은 Momentum과 RMSProp 이 두가지 기법을 사용한다 했습니다.
그렇기에 각각 점화식을 구한 후 합쳐지는 방식으로 구성되어있습니다.

위 수식이 Adam 점화식입니다.
수식안 V(n)과 m(n)은 따로 구해야 하는 가중치 값들입니다.
Adam은 momentum과 RMSProp에서 가져온 것으로 이루어집니다.
먼저 Momentum을 변형한 점화식입니다.
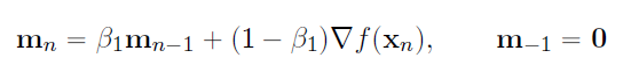
위 수식은 관성의 개념을 탑재한 Momentum과 비슷하지만 RMSProp과 같이
내적하는 식으로 점화식이 구성됩니다.
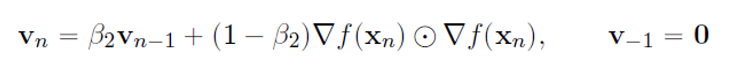
위 수식은 learning rate를 조절한다는 기법인 RMSProp 점화식으로 구성됩니다.
보통 B1=0.9 / B2=0.999로 지정을 합니다.
즉 과거의 값을 더 반영하는 식으로 각각의 가중치들이 계산됨을 의미합니다.
또한 초기 위치에서 m(-1)과 v(-1)은 0이기 때문에
B1,B2를 1에 가깝게 설정하면 과거의 값을 더 크게 반영하는 Adam의 특성상
원점에 편향되게 됩니다.
즉 이 문제를 해결하기 위해 m과 v를 보정해주어야 합니다.
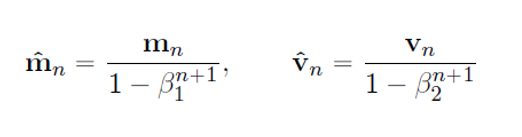
위 식이 M과 V를 보정해주기 위한 식입니다.
만약 B1,B2를 1에 가깝게 설정하게 되면 1 - B1(n+1)은 반대로 작아지게 됩니다.
그 작아진 값에 역수를 취해 m(n)에 곱하였기에 보정한 m(n)은
원점과 멀리있는 점이 됩니다.
(원점에 수렴하는 문제 해결)
v역시 같은 이유 같은 식으로 이루어져있습니다.
코드
class Adam:
"""Adam (http://arxiv.org/abs/1412.6980v8)"""
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None
self.v = None
def update(self, params, grads):
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)
for key in params.keys():
#self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key]
#self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2)
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
#unbias_m += (1 - self.beta1) * (grads[key] - self.m[key]) # correct bias
#unbisa_b += (1 - self.beta2) * (grads[key]*grads[key] - self.v[key]) # correct bias
#params[key] += self.lr * unbias_m / (np.sqrt(unbisa_b) + 1e-7)위 코드는 Adam을 구현한 코드입니다.
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)이 부분은 앞의 optimizer들의 코드구현처럼
초기 위치에는 m과 v값이 0임을 나타냅니다.
lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)이 부분은 점화식과 비교했을 때 직관적인 코드가 아닙니다.
그렇기에 코드와 수식을 연결하기 위해서 유도를 해야합니다.
현재 n번 째라 한다면
self.iter = n + 1
$$lr\_t = \eta \times \frac{\sqrt{1+\beta _{2}^{n+1}}}{1-\beta _{1}^{n+1}}$$
$$ \begin{align*} m_{n+1} &= m_{n} + (1-\beta _{1}) (\Delta f(x_{n}) - m_{n})\\ &= (1 - (1 - \beta_{1})) m_{n} + (1 - \beta_{1}) \Delta f(x_{n})\\ &= \beta_{1}m_{n} + (1 - \beta_{1})\Delta f(x_{n}) \end{align*} $$
$$ \begin{align*} v_{n+1} &= v_{n} + (1 - \beta_{2}) (\Delta f(x_{n}) \odot \Delta f(x_{n}) - v_{n})\\ &= (1 - (1 - \beta_{2})) v_{n} + (1 - \beta_{2}) \Delta f(x_{n}) \odot \Delta f(x_{n})\\ &= \beta_{2} v_{n} + (1 - \beta_{2}) \Delta f(x_{n}) \odot \Delta f(x_{n}) \end{align*} $$
$$\begin{align*} x_{n+1} &= x_{n} - \eta \frac {\sqrt {1 - \beta_{2}^{n+1}}} {1 - \beta_{1}^{n+1}} \frac {1} {\sqrt{v_{n} + 10^{-7}}} \odot m_{n}\\ &= x_{n} - \eta \frac {1} {\sqrt{\frac {v_{n} + 10^{-7}} {1 - \beta_{2}^{n+1}}}} \odot \frac {m_{n}} {1 - \beta_{1}^{n+1}}\\ &= x_{n} - \eta \frac {1} {\sqrt{\hat{v_{n}}}} \odot \hat{m_{n}} \end{align*}$$
다음 식은 Adam점화식이 어떤 과정으로 코드화가 되었는지 보여줍니다.
'딥러닝 > Neural Network' 카테고리의 다른 글
| [딥러닝] Batch Normalization (배치정규화) (0) | 2022.10.27 |
|---|---|
| [딥러닝] LeCun / Xavier / He 초기값 설정 - 표현력 제한, vanishing gradient문제 보완 (4) | 2022.10.01 |
| [딥러닝] 옵티마이저(optimizer) - RMSProp (0) | 2022.09.30 |
| [딥러닝] 옵티마이저(optimizer) - AdaGrad (0) | 2022.09.30 |
| [딥러닝] 옵티마이저(optimizer) - NAG (0) | 2022.09.30 |





