| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- cnn
- Semantic Segmentation
- 딥러닝
- 논문구현
- 옵티마이저
- 코드구현
- 논문리뷰
- Ai
- Self-supervised
- Convolution
- 논문 리뷰
- 프로그래머스
- Computer Vision
- 코딩테스트
- opencv
- pytorch
- ViT
- Python
- optimizer
- 논문
- 파이토치
- 머신러닝
- programmers
- 강화학습
- 파이썬
- Segmentation
- object detection
- transformer
- 알고리즘
- 인공지능
- Today
- Total
Attention please
[딥러닝] 옵티마이저(optimizer) - RMSProp 본문
2022.09.30 - [딥러닝] - 옵티마이저(optimizer) - AdaGrad
옵티마이저(optimizer) - AdaGrad
2022.09.30 - [딥러닝] - 옵티마이저(optimizer) - NAG 옵티마이저(optimizer) - NAG 2022.09.30 - [딥러닝] - 옵티마이저(optimizer) - Momentum 옵티마이저(optimizer) - Momentum 2022.09.29 - [딥러닝] - 옵티..
smcho1201.tistory.com
이전 글에서는 learning rate를 각 스텝마다 변수에 맞게
조절해나가는 optimizer기법인 AdaGrad에 대해 알아보았습니다.
이번에는 AdaGrad에서의 문제점들을 보완한
RMSProp 기법에 대해 알아보겠습니다.
RMSProp
AdaGrad는 스텝이 지나면 지날수록 learnin rate가 줄어듭니다.
그렇기에 스텝이 많이 진행되면 누적치 값인 h(n)이 너무 커져서
학습률이 너무 작아지고 결국 학습이 거의 되지 않는 문제점이 있었습니다.
RMSProp은 이를 보완하기 위해
이전 누적치와 현재 gradient의 좌표별 제곱의 가중치 평균을 하였습니다.
이는 AdaGrad보다 최근의 값을 더 반영하게 해줍니다.
수식
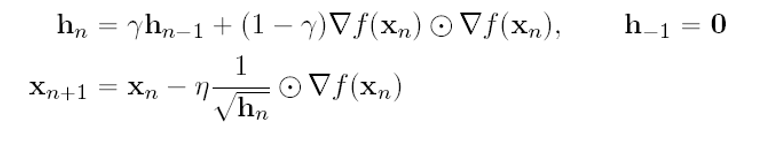
위 수식은 AdaGrad의 점화식과 거의 다를게 없어보입니다.
차이점은 decay rate인 r을 내적하는 식으로 곱해주었다는 것입니다.
r의 값이 클수록 과거의 값을 더 반영하며,
r의 값이 작을 수록 현재의 값을 더 반영하여 계산합니다.
코드구현
class RMSprop:
def __init__(self, lr=0.01, decay_rate = 0.99):
self.lr = lr
self.decay_rate = decay_rate
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] *= self.decay_rate
self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
위 코드는 RMSProp을 코드화 한 것입니다.
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
이 부분은 AdaGrad와 같이 초기 위치의 값에는 과거가 없기 때문에
h(-1) = 0 을 의미합니다.
'딥러닝 > Neural Network' 카테고리의 다른 글
| [딥러닝] LeCun / Xavier / He 초기값 설정 - 표현력 제한, vanishing gradient문제 보완 (4) | 2022.10.01 |
|---|---|
| [딥러닝] 옵티마이저(optimizer) - Adam (0) | 2022.09.30 |
| [딥러닝] 옵티마이저(optimizer) - AdaGrad (0) | 2022.09.30 |
| [딥러닝] 옵티마이저(optimizer) - NAG (0) | 2022.09.30 |
| [딥러닝] 옵티마이저(optimizer) - Momentum (0) | 2022.09.30 |




