| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 딥러닝
- optimizer
- Self-supervised
- 인공지능
- 논문
- 논문리뷰
- Computer Vision
- 옵티마이저
- 코딩테스트
- object detection
- cnn
- pytorch
- ViT
- 논문 리뷰
- 파이토치
- transformer
- programmers
- Segmentation
- 머신러닝
- 파이썬
- Python
- opencv
- 강화학습
- Ai
- 코드구현
- 알고리즘
- 논문구현
- Convolution
- Semantic Segmentation
- 프로그래머스
- Today
- Total
Attention please
[딥러닝] 옵티마이저(optimizer) - NAG 본문
2022.09.30 - [딥러닝] - 옵티마이저(optimizer) - Momentum
옵티마이저(optimizer) - Momentum
2022.09.29 - [딥러닝] - 옵티마이저(optimizer) - SGD 옵티마이저(optimizer) - SGD 옵티마이저란 model을 학습시키기 위해 설정해주어야 하는 작업입니다. SGD를 제외한 옵티마이저들은 모두 SGD의 응용으로..
smcho1201.tistory.com
momentum기법은 현재 위치에서 관성과 gradient의 반대방향을 합하였습니다.
NAG는 momentum을 공격적인 방식으로 변형한 것입니다.
NAG
NAG는 Nesterov Accelated Gradient의 줄임말입니다.
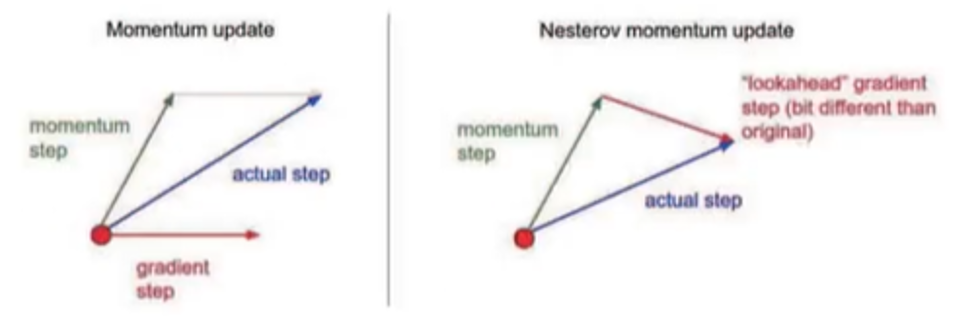
위 사진과 같이 원래 gradient step에 momentum step이 영향을 주어
새로운 방향인 actual step이 생겨 걸어가는 것이 momentum입니다.
하지만 NAG는 현재위치에서의 관성과
관성방향으로 움직인 후의 위치에서의 gradient 반대방향을 합칩니다.
즉 momentum step만큼 걸어간 후
그 위치에서 gradient step만큼 걸어간 위치까지가
actual step이 되는 것입니다.
수식
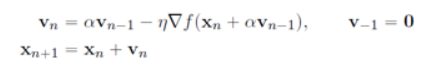
다음 수식을 보면 momentum에서 +∝v(n-1)이 추가 된것을 볼 수 있습니다.
이는 현재 위치에서 momentum step만큼 걸어간 후에 gradient를 구하는 것을 의미합니다.
하지만 x(n)이 아닌 momentum step을 간 위치 즉
다른 점에서 gradient를 구하기 때문에 신경망에서 구현하기 접합하지 않습니다.
그래서 사용된 것이 Bengio의 근사적 접근입니다.
v(n)을 구하기에는 x(n+1)에 대한 정보가 나오기 전이기에v(n)을

으로 바꾸어 나온 식으로 코드화를 진행합니다.
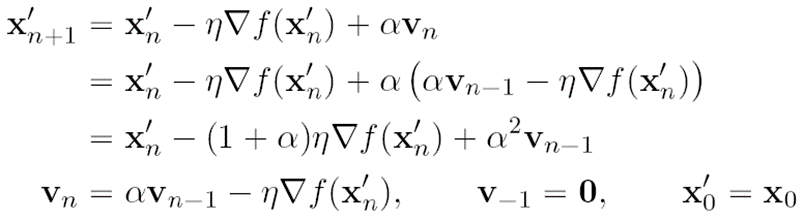
위 수식은 코드화를 할 수 있도록 NAG 수식을 개량한 것입니다.
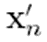
위는 x(n)에서 momentum step후의 위치를 의미합니다.
즉 x(n) 위치에서 momentum 만큼 걸어간 위치를 구하기 위해서 x(n-1)에서 x(n)까지의 속도인 v(n-1)를 구해줍니다.
그리고 v(n-1)에 관성계수를 곱한 후 더하여 나아간 것이x(n)에서 momentum step후의 위치입니다.
그 이후에 momentum만큼 걸어간 위치에서 gradient step만큼 걸어가게 되면x(n+1)의 위치에 오게 됩니다.
그러면 x(n)에서 x(n+1)까지의 속도는 v(n)이 되기때문에x(n+1)위치에서 v(n)에 관성계수를 곱한만큼 걸어간 것이x(n+1)에서 momentum step후의 위치가 됩니다.
코드구현
class Nesterov:
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] *= self.momentum
self.v[key] -= self.lr * grads[key]
params[key] += self.momentum * self.momentum * self.v[key]
params[key] -= (1 + self.momentum) * self.lr * grads[key]
NAG점화식만을 생각하다 코드를 보면
어떤식으로 진행되는지 혼돈이 올 수 있습니다.
self.v[key] *= self.momentum
self.v[key] -= self.lr * grads[key]
이 부분은
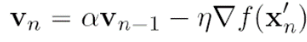
를 의미합니다.
즉 v(n-1)에 momentum 계수를 곱해준 후
gradient step을 밟으라는 의미입니다.
params[key] += self.momentum * self.momentum * self.v[key]
params[key] -= (1 + self.momentum) * self.lr * grads[key]이 코드는

이 식을 의미합니다.
x(n)에서 momentum만큼 걸어간 위치에서
위 코드처럼 update를 하게 되면
x(n+1)에서 momentum step을 간 위치가 나오게 됩니다.
'딥러닝 > Neural Network' 카테고리의 다른 글
| [딥러닝] 옵티마이저(optimizer) - Adam (0) | 2022.09.30 |
|---|---|
| [딥러닝] 옵티마이저(optimizer) - RMSProp (0) | 2022.09.30 |
| [딥러닝] 옵티마이저(optimizer) - AdaGrad (0) | 2022.09.30 |
| [딥러닝] 옵티마이저(optimizer) - Momentum (0) | 2022.09.30 |
| [딥러닝] 옵티마이저(optimizer) - SGD (2) | 2022.09.29 |





