| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- programmers
- 옵티마이저
- 파이썬
- 논문구현
- 논문 리뷰
- cnn
- 코드구현
- transformer
- Computer Vision
- Self-supervised
- 논문리뷰
- opencv
- 파이토치
- Ai
- ViT
- Semantic Segmentation
- Python
- Segmentation
- 인공지능
- 딥러닝
- pytorch
- Convolution
- object detection
- 알고리즘
- 머신러닝
- optimizer
- 논문
- 프로그래머스
- Paper Review
- 코딩테스트
- Today
- Total
Attention please
[논문 리뷰] FAR: Fourier Aerial Video Recognition(2022) 본문
[논문 리뷰] FAR: Fourier Aerial Video Recognition(2022)
Seongmin.C 2023. 12. 25. 05:22이번에 리뷰할 논문은 FAR: Fourier Aerial Video Recognition 입니다.
https://paperswithcode.com/paper/fourier-disentangled-space-time-attention-for
Papers with Code - FAR: Fourier Aerial Video Recognition
🏆 SOTA for Action Recognition on UAV Human (Top 1 Accuracy metric)
paperswithcode.com
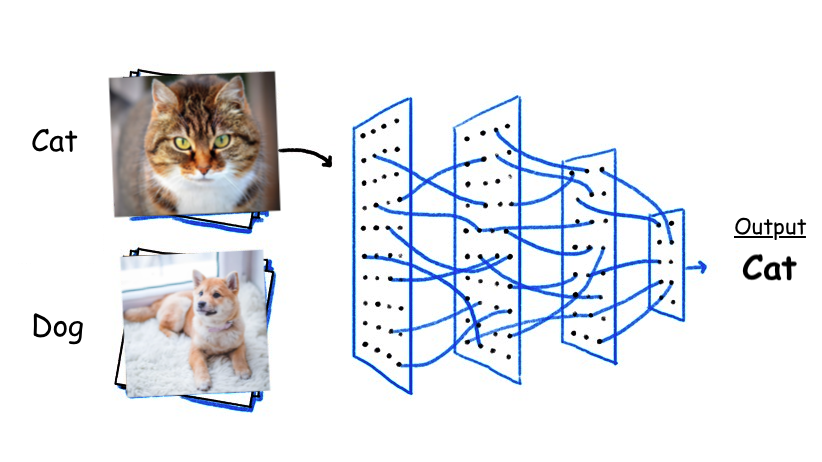
일반적인 image classification 문제의 경우 위 그림과 같이 이미지 내 객체의 class를 분류하는 것을 목표로 하고 있습니다. 이미지 내 객체가 어디에 있는지 위치와 상관없이 종류가 무엇이냐에만 관심이 있죠. 그렇기에 분류를 위해 개발된 CNN모델들은 이미지 데이터의 추상적인 정보를 추출하는데 초점이 맞춰져 있었습니다.
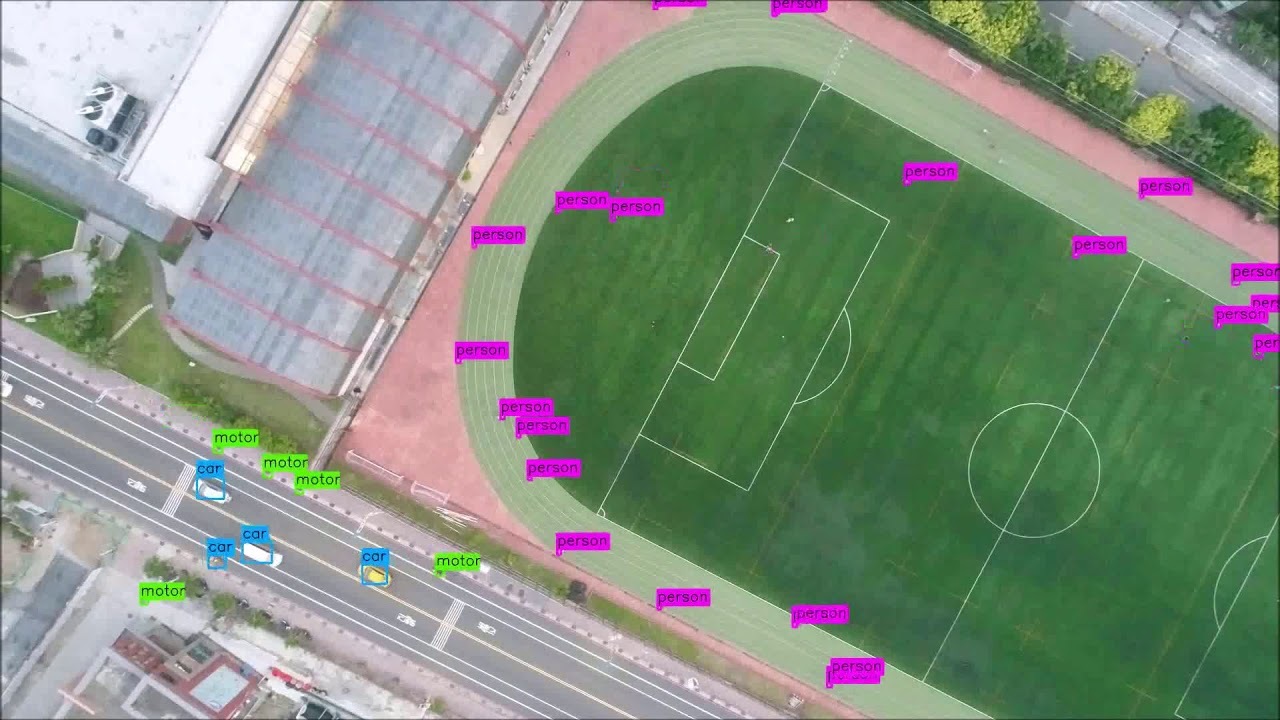
하지만 위의 경우에는 어떨까요? 이미지 내 객체의 크기가 배경에 비해 아주 작고 심지어 움직이기까지 한다면 추장적인 정보에 초점을 맞춰왔던 일반적인 image classification model만으로는 좋은 성능을 기대하기 힘들 겁니다. 결국 객체와 배경을 확실히 분리하여 객체의 존재를 학습할 수 있도록 하는 것이 중요하겠죠.
본 논문은 배경에 비해 작은 객체들을 대상으로 하여 배경에서 분리하기 위해 새로운 Fourier object disentanglement 방법론을 제안합니다. 저자는 푸리에 변환(Fourier Transform) 을 사용하여 작은 객체를 분리해내는데 발생하는 두 가지 문제를 다음과 같이 해결합니다.
- 공간과 객체의 분리를 위해 공간 픽셀의 시간적 변화의 정도를 특성화하기 위해 주파수 도메인에서 작동
- 문맥 정보와 장거리 시공간 종속을 encapsulate하기 위해 network에서 얻은 객체-배경 중첩 특성에 representation을 mapping하기 위해 푸리에 변환의 convolution-multiplocation 속성을 활용
또한 제안된 모델의 경우 UAV 데이터셋의 top-1 accuracy보다 8.02% ~ 38.69% 만큼 높게 나왔으며, 이전 모델에 비해 약 3배 빠른 속도를 보여주었다고 합니다.
여기까지 들으면 이해가 안되겠죠...?
뒤에서 어떻게 문제를 정의했고 어떻게 푸리에 변환을 활용하여 해결하였는지 구체적으로 다뤄보겠습니다.
Introduction
UAV(unmanned aerial vehicle) 는 드론과 같은 무인 항공기를 의미합니다. 이런 UAV가 찍은 영상의 객체는 보통 배경에 비해 픽셀 수나 면적이 훨씬 작기 때문에 얻을 수 있는 정보의 양이 적습니다.

객체의 크기가 배경에 비해 매우 작기 때문에 neural network가 객체의 행동보다 배경에서 더 많은 정보를 추론하게 될 수 있습니다. 배경과 문맥 정보 모두 중요하지만 일단 network가 먼저 객체의 움직임을 식별한 후 판단력있게 객체와 주변 배경의 관계를 추론하도록 해야하죠.
물론 데이터셋에 bounding box와 같은 annotation 정보를 추가하여 object detection으로 문제를 풀어나간다면 성능적으로는 유리할 수 있습니다. 위치 정보를 데이터셋에 제공해주고 있기 때문이죠. 다만 모든 데이터셋에 라벨링을 하기란 실질적으로 거의 불가능에 가깝습니다. 너무 많은 시간 비용이 들죠. 또 다양한 도메인에 일반화하는데 한계가 존재합니다. 결국 객체를 구별할 annotation이 존재하지 않으면, 네트워크는 본질적인 방식으로 움직이는 객체와 배경을 구별할 수 있어야 합니다.
배경과 객체를 분리하는 것 외에도, 네트워크가 문맥 정보와 객체-배경의 관계 및 픽셀 내 관계에 대해 학습하는 것 역시 중요합니다. 이를 위해 아주 유명한 방법론인 self-attention이 존재하죠. self-attention은 이미지 및 비디오 내에서 장거리 종속성을 포착하여 정보를 모델링하는데 유리합니다. 다만 self-attention은 기본적으로 행렬 곱셈에 의해 계산되기에 계산량이 많다는 문제가 존재합니다.
이로써 문제가 정리되었습니다.
- 어떻게 배경과 객체를 분리할 것인가?
- 어떻게 효율적으로 객체와 배경의 문맥적인 정보를 학습할 수 있을까?
Main contributions
저자는 UAV video action 인식을 위해 시간 도메인에서 쉽게 해석되지 않는 신호의 특성에 대한 지식을 포함하는 주파수 스펙트럼에 기반을 두는 새로운 방법론, FAR을 제안합니다. FAR에는 총 두가지 요소가 존재하며, 각 요소들은 위에서 정의한 두개의 문제를 해결하도록 설계되었습니다.
Fourier Object Disentanglement method(FO)
비디오 내의 움직이는 작은 객체는 시간이 지날수록 공간적인 픽셀의 주파수 진폭이 튄다는 특징이 있습니다. 비디오의 공간적 픽셀에 대한 정보를 encoding하는 feature map의 시간적 변화의 크기와 속도를 기반으로 객체의 움직임을 특성화하기 위해 시간 도메인을 주파수 도메인으로 바꾸어 처리하는 푸리에 변환을 응용하여 적용합니다.
Fourier Attention(FA)
객체와 배경의 문맥적인 정보를 추출하는데 self-attention을 사용할 수 있었지만 계산 비용이 크다는 단점이 있었습니다. 이를 위해 제안된 FA는 비디오의 공간-시간 차원에 해당하는 주파수 도메인에서 작동하며, self-attention의 작동 방식을 모방합니다. self-attention의 시간복잡도는 $ O(n^{3}) $ 인 반면 FA의 시간복잡도는 $ O(n^{2}logn) $ 입니다. self-attention에 비해 계산량이 감소되죠. 뿐만 아니라 정확도는 self-attention에 근사하다고 합니다.
이런 FAR의 장점은 다음과 같습니다.
- 전통적인 방법보다 적은 계산을 수행하여 배경과 객체를 분리 및 context encoding의 목표를 달성하기 위해 푸리에 변환의 수학적 성질을 효과적으로 사용
- 학습할 파라미터가 존재하지 않는 무 파라미터 방식
- I3D와 같은 어떤 3D 액션 인식 네트워크에도 내장 가능
- X3D나 I3D 와 같은 3D 액션 인식 백본보다 더 빠르게 수렴
그러면 본 논문의 메인이 되는 FO와 FA의 원리를 자세하게 알아보도록 하겠습니다.
Fourier Object Disentanglement
FO는 자동적으로 객체와 배경을 분리하기 위해 고안된 방법론입니다. 여기서 중요한 건 객체의 움직임인데 이를 공간 픽셀을 encoding하는 feature map의 시간 변화로 특징지을 수 있다는 것입니다. 이 신호 변화의 속도와 크기는 서로 다른 주파수에서 신호의 진폭으로 정량화하는 것이 가능합니다.
feature map을 주파수 공간으로 변환시키기 위해 1D Fourier transform 을 시간 차원에 따라 수행합니다. 해당 연산인 FO가 적용되는 feature map은 다음과 같이 시간과 공간 정보를 담은 형태의 tensor입니다.
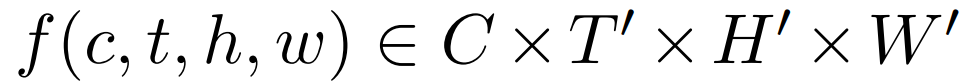
- $ C $ : number of channels
- $ T^{'} $ : temporal dimensions
- $ H^{'} \times W^{'} $ : spatial dimensions
위 feature map의 각각의 픽셀에 대해 고속 푸리에 변환(FFT)을 수행하는 것에 대한 수식은 다음과 같습니다.
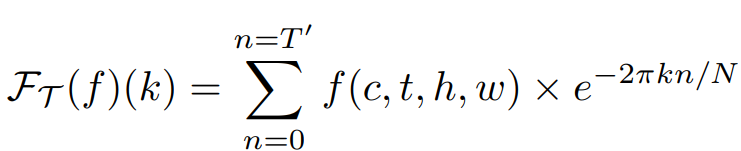
- $ f $ : feature map
- $ k $ : frequency index
- $ n $ : temporal index
- $ N $ : total number of frames
$ \mathcal{F}_{T}(f)(k) $ 은 주파수 k에서의 변환 결과를 나타내며, $ e^{-\frac{2\pi k n}{N}} $ 를 곱해 시간 도메인의 신호를 주파수 성분으로 분해합니다.
기본적으로 시간 차원에서 고주파는 움직임에 해당되며, 저주파는 정적인 영역에 해당됩니다. 이는 움직이는 객체에 해당하는 영역은 높은 주파수와 푸리에 변환의 높은 진폭을 가지게 됩니다.
- 진폭 : 특정 주파수에서 신호의 강도나 크기를 나타냄
- 주파수 : 신호가 얼마나 빠르게 변하는 지를 나타냄
고로 진폭과 주파수를 곱하게 되면 빠른 움직임은 강조되고, 느린 움직임은 억제되어 움직이는 부분과 움직이지 않는 부분을 더 잘 구분할 수 있게 됨을 알 수 있습니다.
위에서 구한 푸리에 변환의 결과인 $ \mathcal{F}_{T}(f)(k) $에 L2-norm을 적용한 $ \left\| \mathcal{F}_{T}(f)(k) \right\|^{2}_{2} $는 주파수 k에서 특정 feature map $ f $의 푸리에 변환의 진폭 제곱을 의미합니다.
다음으로 $ f_{r_k} = \left[ e^{-\frac{2\pi k}{N}} , k = 1 \ldots T' \right] $은 원본 신호에 대한 주파수 응답을 의미합니다. 쉽게 말해 단순 주파수 배열을 의미합니다. 이에 L2-norm을 적용한 $ \left\| f_{r_k} \right\| ^{2}_{2} $은 같은 주파수 k에서 원본 신호의 푸리에 변환 계수를 제곱함을 의미합니다.
최종적으로 푸리에 변환값(진폭)의 제곱을 주파수 배열의 제곱과 곱하여 저주파수(배경)보다 높은 주파수(객체)에 더 높은 가중치를 부여할 수 있도록 합니다.
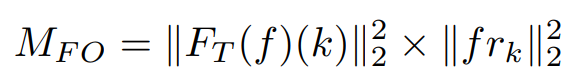
다만 $ M_{FO} $는 움직이는 객체 외에도 움직이는 배경을 포함할 수 있습니다. 때문에 추가 작업으로 $ M_{FO} $를 사용하여 움직이는 객체 픽셀을 움직이는 배경 픽셀에서 구분해주어야 합니다.
움직이는 객체를 더욱더 분리하기 위해, 모델에 의해 계산된 activation maps $ f $를 활용합니다. 이는 완벽하진 않아도 장면의 주요한 지역에서의 활성화가 주요하지 않는 지역보다 높습니다. 즉, $ M_{FO} $와 $ f $를 내적하여 최종 객체 분리 표현을 나타내게 됩니다.

- $ f $ : 시각적으로 중요한 부분을 강조
- $ M_{FO} $ : 동적인 주요 지역이 가장 강조되며, 정적인 비주요 지역은 크게 억제
$ M_{FO} $를 적용한 결과 다음과 같은 순서로 큰 가중치를 매긴다고 합니다.
"동적-중요" > "정적-중요" > "동적-비중요" > "정적-비중요"
시간 복잡도의 경우 다음과 같습니다.
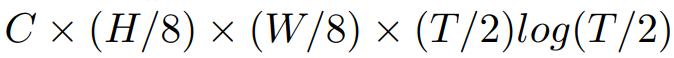
이제 FO를 코드로 구현해봅시다.
shape = x.shape
frequencies = fft.fftfreq(shape[2]).cuda()
fft_compute = fft.fft(x, dim=2, norm='ortho').abs()
입력으로 받는 feature map의 shape은 [batch, channel, temporal, height, width] 입니다. 시간 도메인을 주파수 도메인으로 변환하기 위해 temporal 차원을 슬라이싱하여 FFT를 적용해줍니다. 해당 값은 진폭을 계산하기 위해 사용됩니다.
frequencies = frequencies.unsqueeze(1)
frequencies = frequencies.unsqueeze(1)
frequencies = frequencies.unsqueeze(0)
frequencies = frequencies.unsqueeze(0)
다음으로 단순 주파수 배열을 가져와 shape을 맞춰주는 작업을 진행합니다.
x = x * frequencies * frequencies * fft_compute * fft_compute
마지막으로 진폭과 주파수 배열의 제곱을 곱하여 입력 feature map과 내적을 진행하여 $ F_{FO} $ 를 계산합니다.
class DisEntangle(nn.Module):
def __init__(self, in_channels):
super(DisEntangle, self).__init__()
self.in_channels = in_channels
def forward(self, x):
shape = x.shape
frequencies = fft.fftfreq(shape[2]).cuda()
fft_compute = fft.fft(x, dim=2, norm='ortho').abs()
frequencies = frequencies.unsqueeze(1)
frequencies = frequencies.unsqueeze(1)
frequencies = frequencies.unsqueeze(0)
frequencies = frequencies.unsqueeze(0)
x = x * frequencies * frequencies * fft_compute * fft_compute
return x
최종적인 코드는 위와 같습니다.
Space-Time Fourier Attention

위 사진과 같이 수영하는 사람이 있고 이 사람을 수영장과 분리해야한다고 해봅시다. 위에서 움직임을 주파수 도메인으로 변환하여 객체와 배경을 분리하는 작업을 하였지만 분명 사람 주위에 물결도 같이 움직이면서 배경까지 객체로 잘못 학습할 수 있겠죠. 즉, 수영한다라는 것의 정보를 추출하기 위해서는 전체적인 contextual information을 추출하는 것이 중요합니다. 위에서 말했듯이 contextual information을 추출하는데 유리한 방법은 self-attention 방법론입니다.
다만 self-attention은 계산 비용이 크다는 단점이 존재합니다. 이에 저자는 계산량을 줄이면서 비디오 내의 장거리 공간-시간 관계에 대한 정보를 학습하기 위해 Fourier Space-Time Attention(FA)를 제안합니다.
일반적인 self-attention은 다음과 같이 수행됩니다.
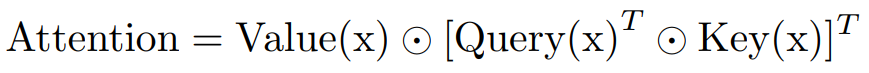
비디오 데이터에는 "시간"과 "공간" 두 가지 독립적인 차원이 존재합니다 ($ C \times T^{'} \times H \times W $) . 이때 $ H \times W $ 2차원 텐서를 벡터화하여, 시간에 따른 공간적 변화를 분석하도록 하기 위해 feature map $ f $의 shape을 $ C \times T^{'} \times (H \times W) $으로 변화시킨 후 2D 푸리에 변환을 수행합니다. 이것이 FA이며, 시간 혹은 공간에 대한 신호를 주파수 도메인으로 변환하는 전통적인 푸리에 변환과 차이가 있다는 점을 확인할 수 있습니다.

- $ m $ : 공간 height 축에 대한 주파수 인덱스
- $ n $ : 공간 width 축에 대한 주파수 인덱스
위와 같이 공간 차원(height, width)가 하나로 합쳐지고, 시간 차원이 그대로 유지된 후에 2D 푸리에 변환이 시간 차원과 합쳐진 공간 차원에 적용되면 다음과 같은 결과를 도출할 수 있다.
- 각 시간 슬라이드(프레임)는 고유한 2D 주파수 스펙트럼을 가진다.
- 이 스펙트럼은 시간에 따라 변하는 공간적 특성을 나타낸다.
- 시간 차원을 유지함으로써 변환된 데이터는 시간적 변화와 공간적 변화를 모두 포착한다.
다음으로 위에서 구한 $ F_{ST} $ 와 그 복소행렬인 $ F_{ST}^{*} $ 을 곱하여 푸리에 변환된 신호에서 특정 주파수 성분의 강도를 측정합니다. self-attention의 attention map과 같은 역할을 한다고 해도 무방합니다.
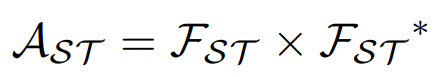
마지막으로 $ A_{ST} $의 역푸리에 변환과 스케일링 조절 하는 $ \lambda_{FA} $를 곱하여 원래의 feature map $ F $를 더해주어 최종적인 Fourier attention 을 구합니다.

본 논문에서 $ \lambda_{FA} $의 경우 실험을 통해 0.01일 때 가장 적합하다고 합니다.
시간복잡도의 경우 self-attention은 query matrix(THW x C)와 key matrix(C x THW)가 곱해질 때 O(C x THW x THW) 의 시간 복잡도를 가지며, 다음 단계인 value matrix(C x HWT) 와 곱해지기에 최종적인 self-attention의 시간복잡도는 O(HWT x HWT x C) 입니다.
반면, FA는 하나의 2D 푸리에 변환과 하나의 역 푸리에 변환을 사용하여 문제를 해결하였기에 self-attention 시간복잡도에 비해 적은 O(C x HWTlog(HWT))를 가집니다.
이제 FA를 코드로 구현해봅시다.
shape = x.shape
fft_compute = fft.fft2(x.view(shape[0], shape[1], shape[2], shape[3]*shape[4]),dim=(2,3), norm='ortho')
fft_compute = torch.conj(fft_compute) * fft_compute # Correlation
feature map을 입력으로 받아 2D 푸리에 변환을 적용시켜줍니다. 시간에 따른 공간적 변화를 분석하도록 유도하기 위해 H x W를 1차원으로 변환하기 위해 view를 사용하여 feature map의 shape을 $ C \times T^{'} \times (H \times W) $ 변환시켜줍니다. 그 후에 $ F_{ST} $ 와 그 복소행렬인 $ F_{ST}^{*} $ 을 곱해줍니다.
fft_compute = fft.ifft2(fft_compute, dim=(2,3), norm='ortho') # Inverse FFT
fft_compute = fft_compute.view(shape[0], shape[1], shape[2], shape[3], shape[4]) # Reshape
위에서 구한 $ A_{ST} $의 역푸리에 변환을 수행한 후 다시 원래의 shape인 ($ C \times T^{'} \times H \times W $) 으로 변환시켜줍니다.
x = x + 0.01 * fft_compute.abs() * x
x #0.01 * torch.real(fft_compute)
마지막으로 $ A_{ST} $의 역푸리에 변환인 $ LF( A_{ST} ) $을 0.01과 곱하여 스케일링 해준 후 feature map과 더하여 $ f_{FA} $를 구합니다.
class SpatialCausality(nn.Module):
def __init__(self, in_channels):
super(SpatialCausality, self).__init__()
self.in_channels = in_channels
def forward(self, x):
shape = x.shape
fft_compute = fft.fft2(x.view(shape[0], shape[1], shape[2], shape[3]*shape[4]),dim=(2,3), norm='ortho')
fft_compute = torch.conj(fft_compute) * fft_compute # Correlation
fft_compute = fft.ifft2(fft_compute, dim=(2,3), norm='ortho') # Inverse FFT
fft_compute = fft_compute.view(shape[0], shape[1], shape[2], shape[3], shape[4]) # Reshape
x = x + 0.01 * fft_compute.abs() * x
return x #0.01 * torch.real(fft_compute)
최종적인 코드는 위와 같습니다.
FAR: Activity Recognition in UAVs
위에서 소개한 FO와 FA를 적용하여 최종적인 FAR 네트워크는 다음과 같습니다.
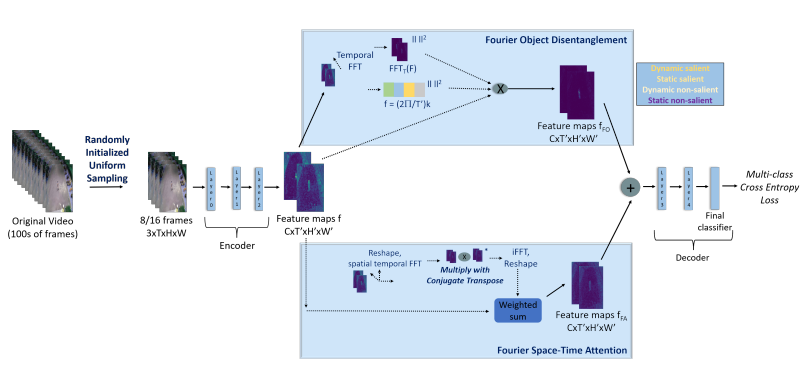
FAR은 다음과 같은 순서로 진행됩니다.
- 입력 비디오에서 8 ~ 16 프레임을 임의로 초기화된 균일 샘플링을 사용하여 샘플링을 진행
- 샘플링된 프레임들은 3D 백본 네트워크(Encoder)의 초반 몇 개의 층을 통과하여 feature map을 생성
- FO와 FA를 병렬적으로 처리하여 각각 $ f_{FO} $와 $ f_{FA} $를 생성한 후 sum
- 신경망의 나머지 계층을 통과하여 최종 동작 분류 확률 분포 생성
Incorporating FO within the 3D backbone
일반적으로, 각 공간 위치에서 시간적 움직임을 포착하기 위해서는 feature map의 시공간 차원이 너무 작지 않아야 합니다. 따라서 맥락적인 정보를 포착하는 일반적인 feature와 고수준의 feature와 미묘한 균형을 이루는 중간 수준의 feature를 사용하여 FO연산을 수행합니다.
Incorporating FA within the 3D backbone
FO를 수행한 후에 네트워크는 배경의 신호를 포함하지 않습니다. 따라서 FA는 FO와 병렬적으로 처리되어야 합니다. 즉, FO와 마찬가지로 중간 수준의 feature를 입력으로 받아 수행됩니다.
전체적인 FAR 네트워크를 코드로 구현해보면 다음과 같습니다.
class DisCaus_Module(nn.Module):
def __init__(self, depth, num_classes, dropout, without_t_stride):
super(DisCaus_Module, self).__init__()
self.model_backbone = I3D_ResNet(depth, num_classes=num_classes, dropout=dropout, without_t_stride=without_t_stride)
pretrained = torch.load('/path/to/pretrained_weight.pth')
pretrained = pretrained["state_dict"]
self.model_backbone.load_state_dict(pretrained)
self.objback_disentangle = DisEntangle(in_channels=512)
self.spatialCaus = SpatialCausality(in_channels=512)
def forward(self, x):
x = self.model_backbone.conv1(x)
x = self.model_backbone.bn1(x)
x = self.model_backbone.relu(x)
x = self.model_backbone.maxpool(x) #64,32,120,68 for input 32, 270, 480
x = self.model_backbone.layer1(x) #256,32,120,68 for input 32, 270, 480
x = self.model_backbone.layer2(x) #512,16,60,34 for input 32, 270, 480
x = self.spatialCaus(x) + self.objback_disentangle(x)
x = self.model_backbone.layer3(x) #1024,8,30,17 for input 32, 270, 480
x = self.model_backbone.layer4(x) #2048,4,15,9 for input 32, 270, 480
num_frames = x.shape[2]
x = F.adaptive_avg_pool3d(x, output_size=(num_frames, 1, 1))
x = x.squeeze(-1)
x = x.squeeze(-1)
x = x.transpose(1, 2)
n, c, nf = x.size()
x = x.contiguous().view(n * c, -1)
x = self.model_backbone.dropout(x)
x = self.model_backbone.fc(x)
x = x.view(n, c, -1)
logits = torch.mean(x, 1)
return logits
def DisCaus(depth, num_classes, dropout, without_t_stride, **kwargs):
model = DisCaus_Module(depth, num_classes=num_classes, dropout=dropout, without_t_stride=without_t_stride)
return model
Results

FAR의 3D backbone으로는 X3D와 I3D를 사용하였으며, 위와 같이 실험을 진행하였습니다. X3D를 백본으로 사용하고, frame개수를 8개, input size를 540x540으로 하였을 때 가장 좋은 성능이 나오는 것을 확인할 수 있었습니다.
또한 FO와 FA를 모두 사용하고 원본 영상의 프레임을 균일 샘플링 추출하였을 때 가장 좋은 성능이 나오는 것을 확인할 수 있습니다.

위 사진을 보면 FO를 적용하기 전에 비해 적용한 후의 결과가 배경 픽셀값을 죽이고 객체에 더 focusing하는 것을 확인할 수 있습니다.
'논문 리뷰 > Image classification' 카테고리의 다른 글
| [논문 리뷰] Swin Transformer: Hierarchical Vision Transformer using Shifted Windows(2021) (2) | 2023.07.28 |
|---|---|
| [논문 리뷰] ViT: AN IMAGE IS WORTH 16X16 WORDS:TRANSFORMERS FOR IMAGE RECOGNITION AT SCALE(2021) (0) | 2023.07.24 |
| [논문 리뷰] EfficientNet(2019), 파이토치 구현 (2) | 2022.12.30 |
| [논문 리뷰] SENet(2018), 파이토치 구현 (0) | 2022.12.29 |
| [논문 리뷰] ResNeXt(2017), 파이토치 구현 (0) | 2022.12.29 |




