| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 논문구현
- Computer Vision
- 코딩테스트
- 파이썬
- object detection
- optimizer
- transformer
- Self-supervised
- 코드구현
- 머신러닝
- cnn
- 알고리즘
- 논문 리뷰
- pytorch
- 파이토치
- 프로그래머스
- 옵티마이저
- Paper Review
- Python
- Convolution
- opencv
- Segmentation
- Semantic Segmentation
- 딥러닝
- 인공지능
- ViT
- programmers
- 논문리뷰
- Ai
- 논문
- Today
- Total
Attention please
타이타닉 - EDA 본문
데이터에는 크게 정형 데이터와 비정형 데이터로 분류된다. 정형 데이터는 보통 머신러닝, 비정형 데이터는 딥러닝으로 처리하는 경우가 대부분인데, 이번에 다룰 데이터는 정형 데이터이다.
비정형 데이터의 경우 딥러닝 즉, 인공신경망까지의 과정에 인간의 노력이 크게 들어가지 않는다. 하지만 정형 데이터의 경우 머신러닝을 적용하기 전 데이터에 대해 충분히 이해를 하여야 하며, 전처리하는 과정이 필요하다.
이와 같이 데이터를 분석하고, 탐색하는 것을 EDA (Exploratory Data Analysis) 라고 하며, 탐색적 데이터 분석이라고도 한다. EDA의 과정은 크게 데이터에 대해 이해를 하고, 관련 도메인 자료 조사를 통해 미리 가설 설정을 하며 시작된다. 가설에 필요한 여러 feature로 필터링을 한 후 값을 출력하여 시각화를 한 후 인사이트를 도출한다. 이를 통해 Valuable information을 창출하는 것이 EDA의 목적이다.
Data
이번 EDA를 한 데이터는 머신러닝의 가장 대표적인 데이터들 중 하나인 타이타닉 데이터이다.
- https://dacon.io/competitions/open/235539/overview/description
- PassengerID : 탑승객 고유 아이디
- Survival : 탑승객 생존 유무 (0: 사망, 1: 생존)
- Pclass : 등실의 등급
- Name : 이름
- Sex : 성별
- Age : 나이
- Sibsp : 함께 탐승한 형제자매, 아내, 남편의 수
- Parch : 함께 탐승한 부모, 자식의 수
- Ticket :티켓 번호
- Fare : 티켓의 요금
- Cabin : 객실번호
- Embarked : 배에 탑승한 항구 이름 ( C = Cherbourn, Q = Queenstown, S = Southampton)
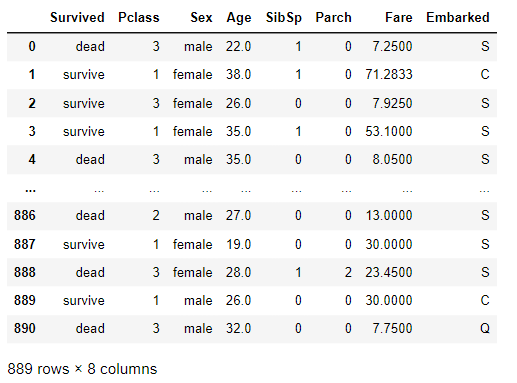
먼저 타이타닉 데이터는 총 12개의 column으로 이루어져 있다. 이중 종속변수는 Survival 1개와 독립변수 11개로 이루어져 있는 것을 볼 수 있다.

위와 같이 데이터가 구성되어 있는데 5개의 행만을 출력했음에도 NaN값이 보인다. 후에 결측치를 처리해야 할 필요가 있어 보인다.

또한 후에 데이터 타입을 변환시켜줄 필요가 있는지 확인하기 위해 각 컬럼의 데이터 타입을 출력시켜보았다.
가설 설정
우선 총 5개의 가설을 세웠다.
- 성별이 남자인 경우 생존률이 높을 것이다.
- 등실의 등급이 높을 수록 생존률이 높을 것이다.
- 나이가 적을 수록 생존률이 높을 것이다.
- 티켓의 요금이 높을 수록 생존률이 높을 것이다.
- 함께 탑승한 가족이 적을 경우 생존률이 높을 것이다.
데이터 전처리
데이터값 Object 변환
종속변수인 Survived 컬럼의 경우 Category column이지만 int형으로 되어있다. (사망 : 0, 생존 : 1)
후에 데이터를 다룰 때 방해가 될 수 있으니 데이터 값을 object로 변환시켜주었다.
change_dict = {0:'dead', 1:'survive'}
data.replace({'Survived':change_dict}, inplace=True)
data['Survived'].unique()
또한 Pclass 컬럼 역시 int형으로 되어있기 때문에 object형으로 변환시켰다.

결측치 확인
아까 데이터를 확인해봤을 때 NaN값이 포함되어 있었다. 먼저 결측치가 어느정도의 비율로 포함되어 있는지 시각화해주었다.

결측치가 포함된 column은 Age, Cabin, Embarked 총 3개이며, Cabin 컬럼의 경우 대부분의 값이 결측치임을 볼 수 있다.
Age 컬럼의 경우 각 데이터의 중앙값으로 결측값을 대체하였고, Embarked 컬럼의 경우 2개뿐이 없기 때문에 결측치가 존재하는 행 2개를 제거 시켰다. 하지만 Cabin 컬럼은 결측치가 너무 많이 포함되어있어, 컬럼 자체를 제거해주었다.
# Cabin 컬럼 삭제
data = data.drop('Cabin', axis = 1)
# Age 컬럼 결측치 중앙값 대체
data['Age'].fillna(data['Age'].median(), inplace=True)
# Embarked 컬럼의 결측치 행 제거
data = data.drop(index = data[data['Embarked'].isnull()].index, axis = 0)
# 결측치 확인
print(f"데이터 개수 : {len(data)}")
print(len(data) - data.count())

특정 column 제거
다음으로 의미없는 컬럼을 제거해주었다.
Passengered, Ticket, Name 컬럼의 경우 종속변수에 영향이 크게 없어 보여 제거해주었다.
이상치 탐색
이상치 데이터는 오히려 모델의 성능을 떨어뜨릴 수 있기 때문에 제거해주어야 한다. 하지만 어디까지 이상치로 봐야하는지 기준이 필요하다. 이번에 사용한 방법은 IQR(Inter Quantile Range) 기법을 사용하였다.
IQR 방식은 사분위 중 Q1과 Q3를 IQR이라 칭하며, IQR에 1.5을 곱하여 Q3에 더한 지점을 최댓값, Q1에 빼준 지점을 최솟값으로 한다.
def remove_outliers(data, column):
num = data[column]
Q1 = num.quantile(.25)
Q3 = num.quantile(.75)
IQR = Q3 - Q1
return num[(Q1-1.5*IQR > num)|(Q3+1.5*IQR < num)]
확인 결과 이상치가 존재하는 column의 종류는 Age, SibSp, Parch, Fare 총 4개가 있었다. 하지만 나이의 경우 이상치라 보기엔 어려우며, 같이 탑승한 가족의 수와 티켓의 가격은 높은 경우가 드물지만 이 역시 종속 변수에 영향을 주는 데이터의 특징으로 볼 수 있기 때문에 이상치라 보기 힘들다.
이러한 이유로 따로 이상치를 제거하는 작업은 하지 않았다.
Target 확인
target변수인 Survived 컬럼이 어떤 비율로 분포되어있는지 시각화 하였다.
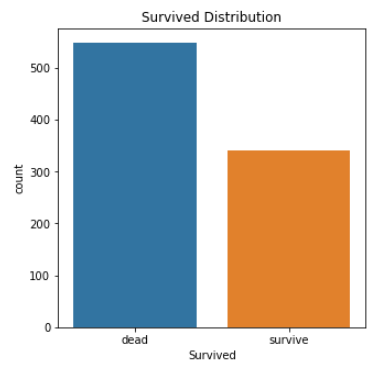
다음과 같이 생존에 비해 사망의 비율이 더 높은 것을 볼 수 있다.
Column 분포 확인
Categorical Column
Column은 크게 카테고리 형과 연속형 으로 나눠진다. 먼저 카테고리형 컬럼을 확인해 주었다.
# categorical column
cate_col = []
for col in data.columns:
if data[col].dtype == object:
cate_col.append(col)
print('==========================================================')
print(f"{col} : {data[col].unique()}")
print(f"{data[col].value_counts()}")
print()
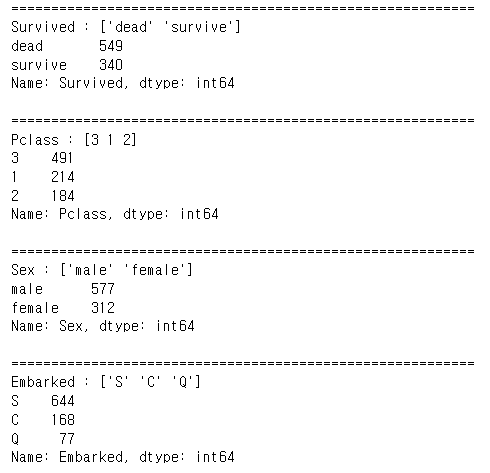
카테고리 형의 컬럼은 총 4개가 있었으며, 위와 같은 비율로 분포되어있다.
다음으로 Survived 컬럼과 Categorical 컬럼의 비율을 시각화하였다. 두 변수 모두 Categorical 컬럼이므로 bar그래프와 모자이크 plot을 그려주었다.

위 plot을 보고 나온 결론은 다음과 같다.
- 등실의 등급이 높을 수록 생존률이 증가합니다.
- 성별이 남자인 경우 생존률이 크게 줄어듭니다.
- Southampton 항구에 탑승한 승객들의 생존률이 상당히 낮은 반면 나머지 두항구의 생존률은 적당히 보장됩니다.
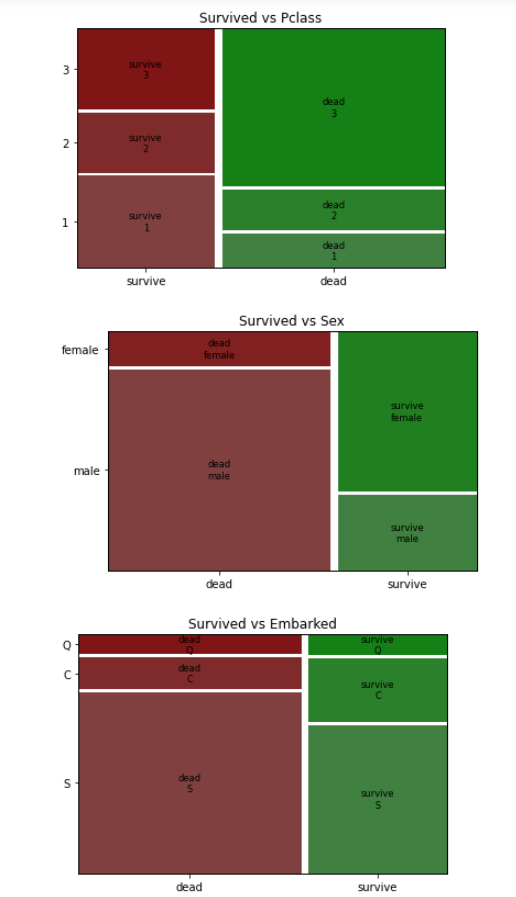
모자이크 plot을 보니 등실의 등급이 생존률보다 사망률에 더 큰 영향을 미치는 것을 확인할 수 있다.
Continuous Column
# continuous column
con_col = []
for col in data.columns:
if data[col].dtype != object:
con_col.append(col)
print(f"{col} : {data[col].nunique()}")
print('=============================================')
print()

연속형 컬럼 역시 4개가 존재했으며, Survived 변수와 비교를 시각화하였다.


위 plot을 보고 나온 결론은 다음과 같다.
- 20대, 30대의 경우 사망률이 증가한다.
- 함께 탑승한 가족의 수는 사망률과 연관이 없어보인다.
- 티켓의 값이 저렴할 수록 사망률은 높아진다. -> 등실의 등급과 연관
컬럼 삭제
위에서 각 컬럼과 target 변수를 비교해보았고 함께 탑승한 가족의 수와 생존률은 크게 연관이 없어 보인다는 인사이트를 얻을 수 있었다. 바로 가족의 수를 나타내는 SibSp와 Parch 컬럼을 제거해주자.
data.drop(['SibSp', 'Parch'], axis = 1, inplace = True)
print(f"shape : {data.shape}")
data.head()
상관 관계
각 열의 상관계수 출력
상관계수를 출력하기 위해 피어슨 상관계수를 사용하였다. (두 변수 간의 선형 상관관계를 계량화한 수치)
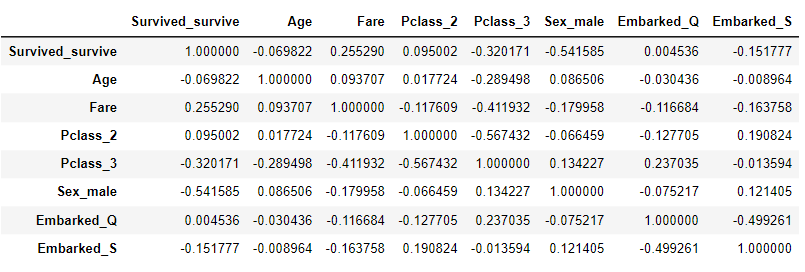
Visualize
위에서 출력한 데이터프레임으로 히트맵을 그려 시각화 해주었다.
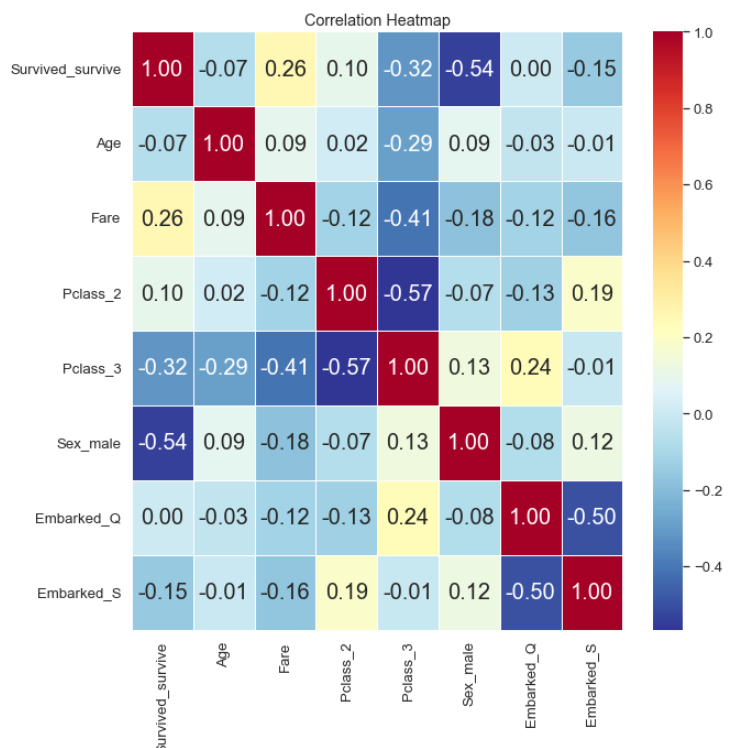
하지만 히트맵 만으로는 정확하게 비교하기 어려울 수 있기 때문에 상관계수가 0.4 이상이거나 -0.4 이하인 column에 대해서만 따로 출력을 해주어 비교해주었다.
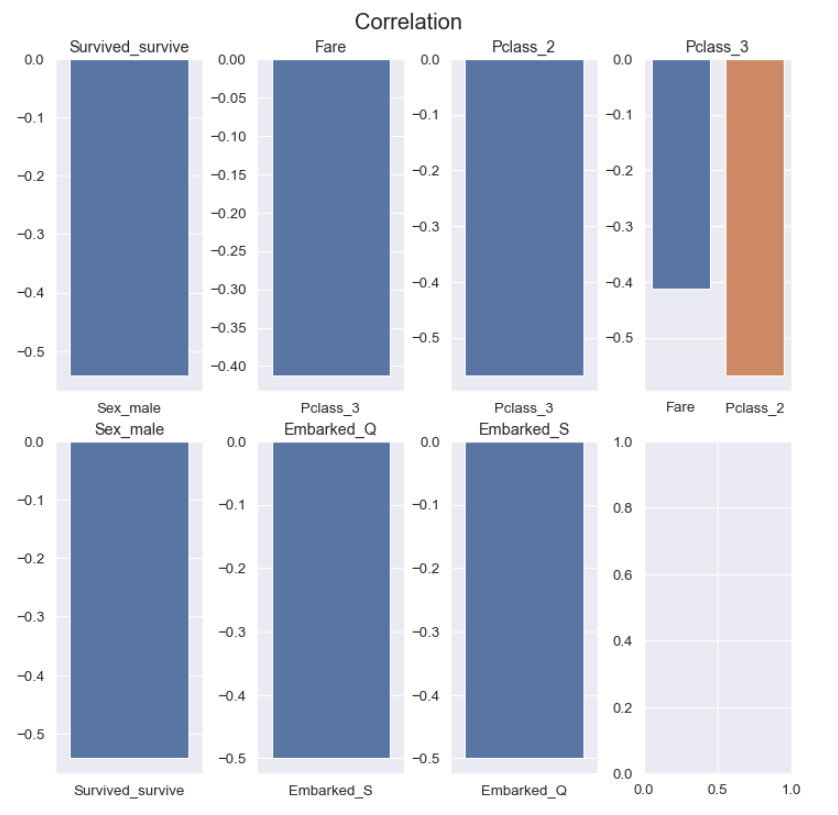
다음으로 종속변수와 상관계수를 비교해주었다.

위 그림을 통해 Sex, Pclass, Fare 변수가 종속변수와 높은 상관관계를 가지는 것을 확인할 수 있다.
VIF 확인
독립변수는 종속변수와만 상관관계가 있어야 한다.
만약 독립변수가 종속변수 뿐만 아닌 다른 독립변수와의 상관관계도 높다면 그것을 다중공선성이라 부르며, 이와 같은 경우 정확한 회귀분석을 하는 것이 어려워진다.
독립변수의 다중공선성을 확인하기 위해 VIF를 사용하였다.

보통 VIF 값이 10미만인 column은 다중공선성이 없다고 판단한다. 위 그림을 보아도 대부분의 column의 VIF값이 10 미만임을 확인할 수 있다.
10이상의 값을 가지는 column은 Pclass 변수인데 이는 Fare변수와 관련이 높기 때문에 높게 나온것으로 보인다.
가설 확인
지금까지의 도출한 인사이트를 토대로 위에서 세웠던 가설을 확인해 볼 차례이다. 첫 번째 가설부터 살펴보자.
1. 성별이 남자인 경우 생존률이 높을 것이다.
성별에 대한 컬럼인 Sex 컬럼과 Survived 컬럼을 bar plot으로 비교해주었다.
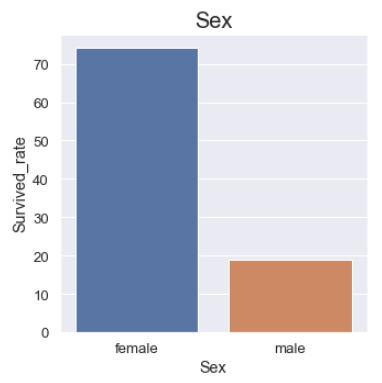
성별이 여성인 경우 남성에 비해 생존률이 압도적으로 높았다. 가설을 세울때 신체적 조건때문에 남성의 생존률을 높게 잡았는데 아무래도 Lady First의 나라인 영국쪽이다 보니 또 일리가 있는 인사이트로 보인다.
- 여성 : 74%
- 남성 : 18%
2. 등실의 등급이 높을 수록 생존률이 높을 것이다.
등실의 등급에 관련된 컬럼은 Pclass이다. Pclass 변수와 Survived 변수를 bar plot으로 비교해주었다.

등실의 등급이 3등급에서 1등급으로 올라갈 수록 생존률이 올라가는 것을 확인할 수 있다.
- 1 : 62%
- 2 : 47%
- 3 : 24%
3. 나이가 적을 수록 생존률이 높을 것이다.
나이의 경우 관련 컬럼은 Age이다. 하지만 Age는 연속형 컬럼이므로 비교를 위해 6등분을 하여 비교하였다. 6등분의 비율은 모두 동일하게 하여 나누어 주었다.
data['Age_dist'] = pd.cut(data['Age'], 6, labels=[0, 1, 2, 3, 4, 5]).astype(object)
data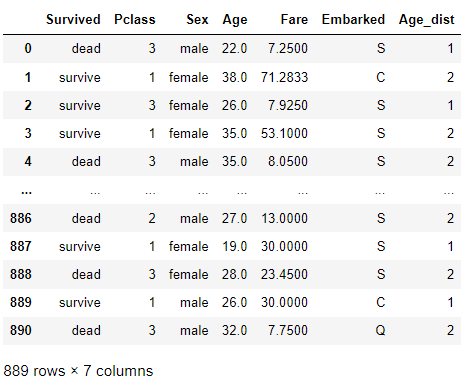
새로 만든 Age_dist 컬럼과 Survived 컬럼을 bar plot으로 비교해주었다.
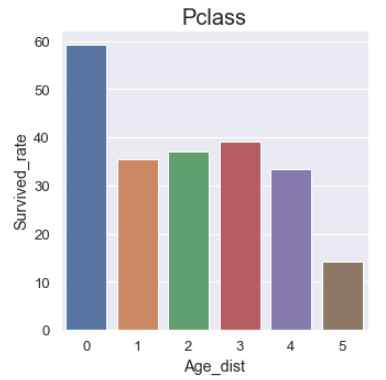
나이가 적어질 수록 생존률이 높아졌다. (이 역시 젠틀의 나라인 영국의 사회적 약자를 배려해주는 문화가 영향을 끼치는 것으로 보인다.)
- 0 : 59%
- 1 : 35%
- 2 : 37%
- 3 : 39%
- 4 : 33%
- 5 : 14%
나이가 적을 수록 생존률이 높다는 인사이트가 존재하기 때문에 이를 통해 파생변수 하나를 만들 수 있다. 총 나이의 중앙값을 구하면 28이 나오는데 이를 통해 28살 이상을 1, 미만을 0으로 주어 새로운 변수를 생성해주었다.
data['Low_Age'] = np.where(data.Age <= 28, 1, 0)
data['Low_Age'] = data['Low_Age'].astype(object)
4. 티겟의 요금이 높을 수록 생존률이 높을 것이다.
티겟의 요금에 대한 컬럼은 Fare 이기 때문에 Survived, Fare 변수를 비교해주었다.
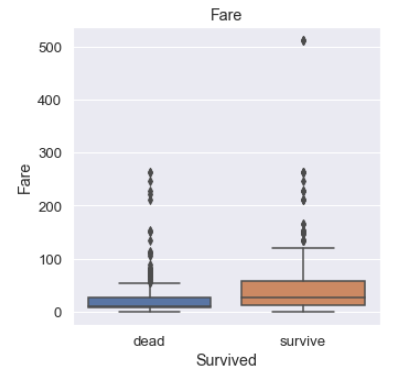
Fare값이 올라갈 수록 생존률이 높아졌다. 또한 Survive boxplot의 중앙값이 dead boxplot보다 위에 위치하며, Survive boxplot의 크기가 더 큰 것으로 보아 분포 역시 넓은 것으로 보인다. 즉, Fare값은 생존률에 영향을 준다.
Fare 변수 역시 생존률에 영향을 미치기 때문에 새로운 변수를 추가해주었다. Fare 변수의 중앙값은 26이기 때문에 26이상은 1, 미만은 0으로 하여 새로운 변수를 생성해주었다.
data['Low_Fare'] = np.where(data.Fare <= 26, 1, 0)
data['Low_Fare'] = data['Low_Fare'].astype(object)
5. 함께 탑승한 가족이 적을 경우 생존률이 높을 것이다.
위에서 함께 탑승한 가족에 대한 정보는 종속변수와 연관성이 떨어져 제거해주었다.
Feature Engineering
위에서 추가한 파생변수들과 Age변수를 제거해주어 데이터를 완성하였다.
data.drop(['Age'], axis = 1, inplace = True)
data
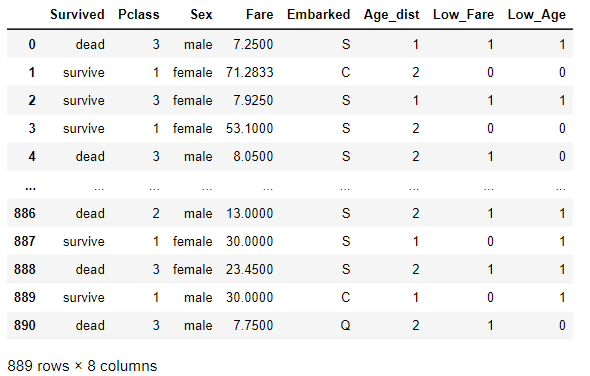
'머신러닝' 카테고리의 다른 글
| 클러스터링 ; 데이터 전처리 - (2) (0) | 2023.02.17 |
|---|---|
| 클러스터링 ; 데이터 살펴보기(EDA) - (1) (0) | 2023.02.17 |
| sklearn의 Simplelmputer으로 결측치 채우기 (0) | 2023.02.09 |


