| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- ViT
- 강화학습
- pytorch
- Self-supervised
- Computer Vision
- 인공지능
- 논문구현
- opencv
- Convolution
- programmers
- Python
- Segmentation
- 옵티마이저
- 코딩테스트
- 머신러닝
- Semantic Segmentation
- 프로그래머스
- Ai
- 논문 리뷰
- 알고리즘
- 딥러닝
- 논문리뷰
- 코드구현
- optimizer
- transformer
- 파이썬
- 파이토치
- object detection
- 논문
- cnn
- Today
- Total
Attention please
이진탐색트리(최소키/최대키 탐색, 노드 삭제, 트리순회) 본문
최소키 탐색
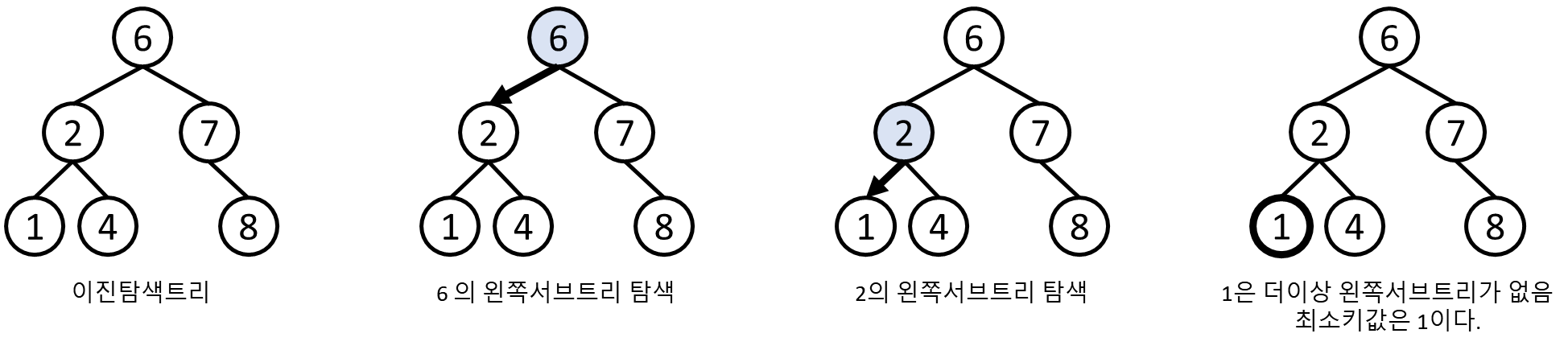
최소키 탐색이란 이진탐색트리에서
키 값이 가장 작은 노드를 찾는 것을 의미합니다.
이진탐색트리 특성 상 작은 키 값은 왼쪽에 있기에
루트의 왼쪽서버트리를 반복적으로 탐색을 하여 최소키를 탐색합니다.
최대키 탐색
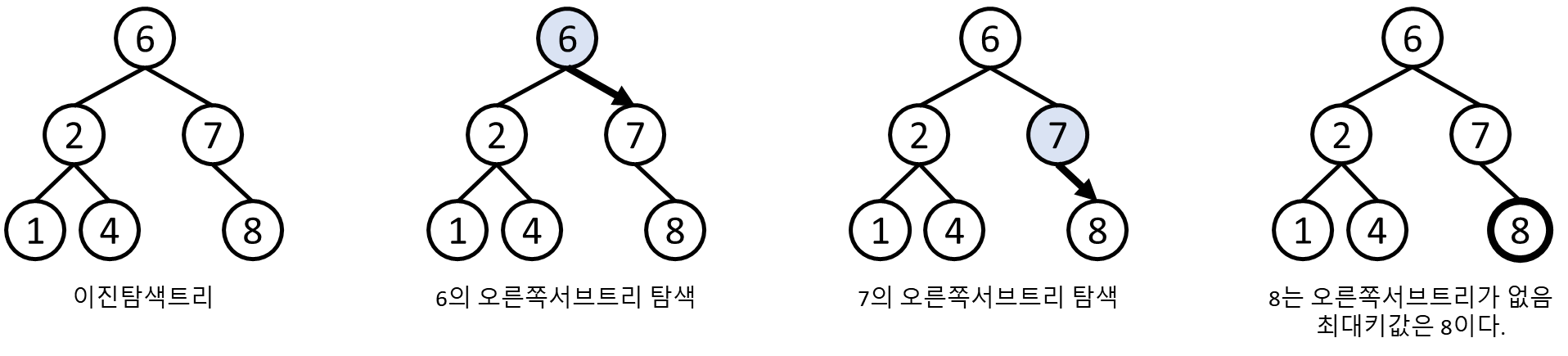
최대키 탐색이란 키 값이 가장 큰 노드를 찾는 것을 의미합니다.
이 역시 이진탐색트리의 특성 상 큰 키 값은 오른쪽에 있기에
루트의 오른쪽 서버트리를 반복적으로 탐색하여 최대키를 탐색합니다.
최소키 / 최대키 탐색 구현
총 2개의 메소드가 사용됩니다.
min_node() : 서브트리에서 최소키 값을 가지는 노드 리턴
max_node() : 서브트리에서 최대키 값을 가지는 노드 리턴
def min_node(self, sroot):
# 서브트리에서 최소키값을 가지는 노드 리턴
if not sroot:
return None
else:
if sroot.left:
return self.min_node(sroot.left)
else:
return sroot
def max_node(self, sroot):
# 서브트리에서 최대키값을 가지는 노드 리턴
if not sroot:
return None
else:
if sroot.right:
return self.max_node(sroot.right)
else:
return sroot
노드 삭제
노드 삭제는 총 3가지의 경우를 생각해야 합니다.
1. 자식 노드가 없는 노드를 삭제하는 경우
2. 자식노드가 1개인 노드를 삭제하는 경우
3. 자식노드가 2개인 노드를 삭제하는 경우
1. 자식노드가 없는 노드를 삭제
다음과 같은 경우에는 먼저 삭제될 노드를 탐색합니다.
그 후에 부모노드를 이용하여 삭제합니다.
예시로 주어진 이진탐색트리에서 자식이 없는 노드 3을 삭제하겠습니다.

2. 자식노드가 1개인 노드를 삭제
이 경우에는 삭제할 노드의 자식노드를
삭제할 노드의 부모노드와 연결합니다.
예시로 자식 노드가 1개인 노드 7을 삭제하겠습니다.

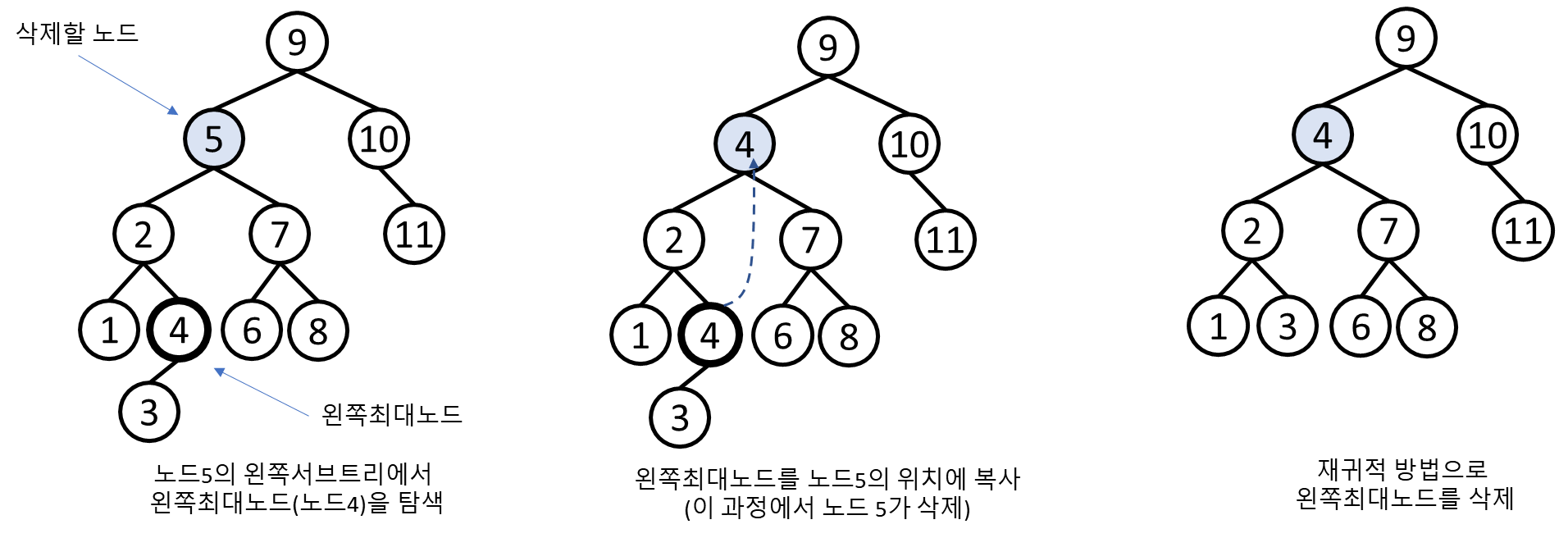
3. 자식노드가 2개인 노드를 삭제
이 경우에는 삭제할 노드의 왼쪽 서브트리에서
키 값이 가장 큰 노드를 탐색합니다.
이때 찾은 왼쪽최대노드의 키와 값을 삭제할 노드에 복사합니다.
(위 과정으로 삭제할 노드는 삭제됩니다)
마지막으로 왼쪽최대노드를 삭제합니다.
예시로 자식 노드가 2개인 노드 5를 삭제하겠습니다.
노드 삭제 구현
총 2가지의 메소드가 사용됩니다.
delete() : 전체트리에서 노드 삭제
delete_in_subtree() :
서브트리에서 특정 key값을 가지는 노드 삭제
삭제 후 왼쪽서브트리의 루트노드 리턴
def delete(self, key):
# 전체트리에서 노드 삭제
self.root = self.delete_in_subtree(key, self.root)
def delete_in_subtree(self, key, sroot):
if not sroot:
return
if key < sroot.key:
# 왼쪽 서브트리에서 삭제
sroot.left = self.delete_in_subtree(key, sroot.left)
elif key > sroot.key:
# 오른쪽 서브트리에서 삭제
sroot.right = self.delete_in_subtree(key, sroot.right)
else: # key == sroot.key
if sroot.left and sroot.right: # 자식이 두개
# 서브트리의 루트노드를 왼쪽서브트리의 최대노드로 교체
max_node = self.max_node(sroot.left) # 왼쪽에서 최대키값을 가지는 노드
sroot.key = max_node.key
sroot.value = max_node.value
# 왼쪽서브트리에서 최대 노드를 삭제
sroot.left = self.delete_in_subtree(max_node.key, sroot.left)
elif sroot.left: # 왼쪽 자식만 있는 노드 삭제
sroot = sroot.left
elif sroot.right: # 오른쪽 자식만 있는 노드 삭제
sroot = sroot.right
else: # 자식이 없는 노드 삭제
sroot = None
return sroot
트리순회
깊이우선탐색(DFS)을 할 때 서브트리를 재귀적으로 순회를 하는데,
3가지의 방법으로 순회를 합니다.

순회방법이 3가지가 존재하므로
서브트리를 순회하는 메소드역시 총 3가지입니다.
중위순회
def inorder(self, sroot):
if sroot:
self.inorder(sroot.left)
print(sroot.key, end=' ')
self.inorder(sroot.right)
전위순회
def preorder(self, sroot):
if sroot:
print(sroot.key, end = ' ')
self.preorder(sroot.left)
self.preorder(sroot.right)
후위순회
def postorder(self, sroot):
if sroot:
self.postorder(sroot.left)
self.postorder(sroot.right)
print(sroot.key, end = ' ')
너비우선탐색(BFS)를 할 때,
큐를 이용하여 레벨순서대로 순회를 합니다.
레벨순회 알고리즘에 대해 설명을 하자면
1. 큐에서 노드 하나를 꺼낸다.
2. 노드를 방문한다.
3. 해당 노드의 자식들을 큐에 넣는다.
로 진행됩니다.
그렇다면 큐를 이용하여 레벨순회하는 것을 코드로 구현해보겠습니다.
def levelorder(self, sroot):
queue = deque()
queue.append(sroot)
while queue:
node = queue.popleft()
if node:
print(node.key, end = ' ')
queue.append(node.left)
queue.append(node.right)
지금까지 트리순회 총 4가지에 대해 알아보았습니다.
(중위순회 / 전위순회 / 후위순회 / 레벨순회)
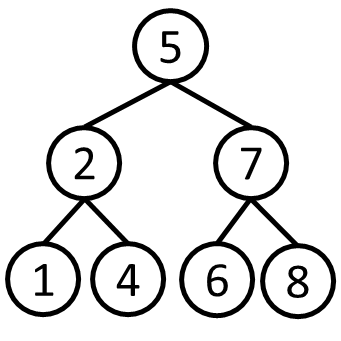
이번에는 위 트리를 4가지 방법으로 순회를 하였을 때
어떤 순서로 정렬이 될지 비교해보겠습니다.
중위순회
[1 2 4 ] 5 [6 7 8]
전위순회
5 [2 1 4] [7 6 8]
후위순회
[1 4 2] [6 8 7] 5
레벨순회
5 2 7 1 4 6 8
이진탐색트리를 중위순회하면 정렬된 결과가 나온다는 특징도 있습니다.
단점
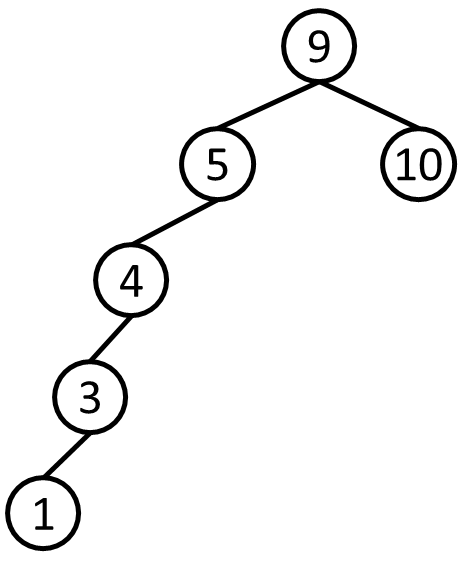
다음 그림과 같이 이진탐색트리의 형태가 한쪽으로 치우쳐지게 되면
탐색 / 삽입 / 삭제 연산의 시간복잡도가 O(N) 에 가까워지게 됩니다.
위 단점을 보완하기 위해서는
한쪽으로 치우치지 않은 트리의 모양을 유지하여야 하는데,
이때 사용되는 것이 "AVL트리", "레드-블랙 트리" 가 있습니다.
정리

'알고리즘' 카테고리의 다른 글
| 이진탐색트리(노드 구현, 삽입, 탐색) (0) | 2022.11.25 |
|---|---|
| 이진트리(binary tree) & 트리탐색(BFS, DFS) (0) | 2022.11.24 |
| 자료구조 - 트리, 트리용어 (0) | 2022.11.23 |
| 탐색 알고리즘(선형, 이진, 해시) (0) | 2022.11.11 |
| 스택 (0) | 2022.10.07 |




