| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- object detection
- Self-supervised
- ViT
- 머신러닝
- 논문 리뷰
- 딥러닝
- 파이썬
- 코드구현
- cnn
- pytorch
- 파이토치
- 논문구현
- 인공지능
- Paper Review
- Python
- Semantic Segmentation
- 알고리즘
- 코딩테스트
- Convolution
- programmers
- 논문리뷰
- optimizer
- 옵티마이저
- 프로그래머스
- Computer Vision
- opencv
- transformer
- Segmentation
- Ai
- 논문
- Today
- Total
Attention please
탐색 알고리즘(선형, 이진, 해시) 본문
탐색 알고리즘이란
저장된 데이터에서 특정 조건을 만족하는 데이터를 찾는 알고리즘을 의미합니다.
즉, 저장된 데이터들 중에 원하는 값을 찾는 탐색문제에서 사용됩니다.
키(key)
탐색 문제에서 주목하는 항목을 키(key)라고 합니다.
데이터값이 그대로 키 값이 될 수도 있습니다.
ex) 탐색조건 : '국적이 한국인 사람을 찾습니다.'
키 : 국적
선형 탐색
선형(직선)으로 늘어선 데이터에서 원하는 키 값을 가진 원소를 찾을 때까지
맨앞에서부터 순서대로 검색하는 알고리즘입니다.
만약 검색할 값과 같은 원소를 찾게 되면
검색을 성공함과 동시에 알고리즘은 종료하게 됩니다.

만약 검색할 값을 찾지 못하고 배열의 맨 끝을 지나간 경우
검색을 실패함과 동시에 알고리즘은 종료하게 됩니다.

만약 탐색에 성공하면 인덱스를 리턴하며,
검색에 실패하면 -1을 리턴합니다.
def linear_search(seq, target):
for i in range(len(seq)):
if seq[i] == target:
return i
return -1
print(linear_search([6,4,3,2,1,2,8], 2))
## -> 3
print(linear_search([6,4,3,2,1,2,8], 5))
## -> -1
선형 탐색의 시간복잡도는 O(N)입니다.
이진 탐색
이진 탐색은 반드시 정렬된 상태에서 시작해야 합니다.
정렬된 데이터의 중간을 기준으로 두 부분으로 나누어 탐색하며,
선형 탐색보다 빠르게 탐색이 가능합니다.
이진 탐색으로 66이라는 값을 탐색하려고 한다면
우선 데이터를 정렬시킨 후 중간 값을 검색합니다.

위 데이터에서는 40이 중간값이며, 40 < 66 이므로,
다음 검색 범위는 (M+1, R) 이 됩니다.

이 검색범위 중 중간값은 69이며, 69 > 66 이므로,
다음 검색 범위는 (L, M-1) 입니다.

이번 중간값은 54이며, 54 < 66 이므로,
다음 검색 범위는 (M+1, R) 입니다.

중간 값인 M 이 탐색해야하는 값인 66이므로,
알고리즘을 종료합니다.
위와 같이 이진 탐색은 탐색을 반복할 때마다
검색 범위가 절반으로 줄어들게 됩니다.
이진 탐색을 반복적 이진탐색과 재귀적 이진탐색으로 코드를 구현해보겠습니다.
<반복적 이진탐색>
def binary_search_iter(seq, target):
left = 0 # 검색 범위 맨 왼쪽 인덱스
right = len(seq) - 1 # 검색 범위 맨 오른쪽 인덱스
while left <= right:
mid = (left + right) // 2 # 중앙의 원소 위치
if seq[mid] == target:
return mid # 검색 성공
elif seq[mid] > target:
right = mid - 1 # 검색 범위를 왼쪽 절반으로 줄임
else:
left = mid + 1 # 검색 범위를 오른쪽 절반으로 좁힘
return -1 # 검색 실패
nums = sorted([6,4,3,2,7,8])
print(binary_search_iter(nums, 3))
## -> 2
print(binary_search_iter(nums, 3))
## -> -1
<재귀적 이진탐색>
def binary_search_recursive(seq, target):
def recur(left, right):
if left > right:
return -1
mid = (left + right) // 2
if seq[mid] == target: # 타겟 발견
return mid
elif seq[mid] > target:
return recur(left, mid-1) # 왼쪽 파트 검색
else:
return recur(mid+1, right) # 오른쪽 파트 검색
return recur(0, len(seq)-1) # recur() 함수 호출
nums = sorted([6,4,3,2,1,7,8])
print(binary_search_iter(nums, 3))
## -> 2
print(binary_search_iter(nums, 3))
## -> -1binary_search_recursive() 함수는
recur() 인 재귀함수를 사용하여 target의 인덱스를 리턴합니다.
이진 탐색의 시간복잡도는 O(logN) 입니다.
선형 탐색은 처음 위치부터 끝까지 탐색을 해야하지만
이진 탐색은 한 번 탐색을 할 때마다 데이터가 줄어들기에 더 효율적입니다.

해시 탐색
해시 탐색이란
해싱을 이용하여 매우 빠르게 데이터를 검색하는 방법입니다.
해시의 시간복잡도는 평균적으로 O(1)이 걸리며,
정말 최악의 경우 O(N)이 나오기도 하지만 확률이 극악으로 적습니다.
파이썬을 사용한다면 딕셔너리를 이용하여 해시 탐색을 하는 것이 가능합니다.
해싱(hashing)이란,
키를 해시 함수를 이용하여 배열의 인덱스로 변환하여 데이터를 저장하는 방법입니다.
해시 함수란,
키를 인덱스(0 이상의 정수)로 변환시키는 함수입니다.
해시값(해시주소)란,
해시 함수가 계산한 값을 의미합니다.
해시 테이블이란,
데이터를 해시값에 따라 저장한 배열을 의미합니다.

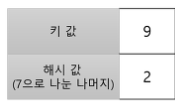
만약 다음과 같은 데이터가 주어졌으며

해시 함수가 7으로 나눈 나머지라 한다면,

다음과 같이 키 값들은 인덱스를 가지게 됩니다.
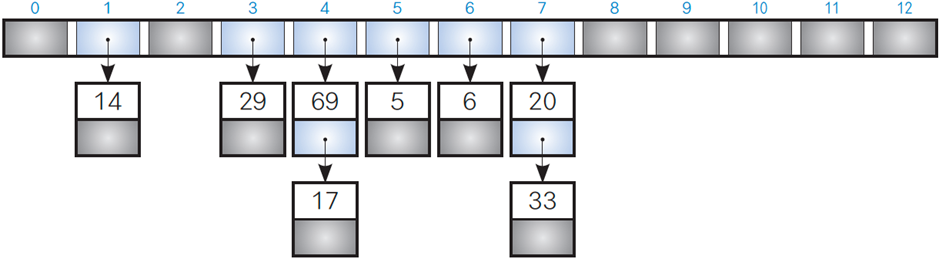
이때 서로 다른 키들이 동일한 해시값을 가질 때 충돌이 발생하며,
이를 해시 충돌이라 합니다.
해시 충돌을 해결하기 위한 방법을 소개하겠습니다.
<체인법>
같은 해시 값을 갖는 요소들을 연결리스트로 관리합니다.
<오픈주소법>
같은 해시 값의 데이터가 다른 버킷에 저장되어 있으면
재해싱해서 원하는 값을 찾을 때까지 재해시를 반복합니다.

이번에는 파이썬의 딕셔너리를 사용하여
해시 알고리즘을 사용하겠습니다.
n = 10000
nums = list(range(n))
dict_nums = {}
for i in range(n):
dict_nums[i] = i
#######
for i in range(len(nums)):
i in dict_nums
'알고리즘' 카테고리의 다른 글
| 이진트리(binary tree) & 트리탐색(BFS, DFS) (0) | 2022.11.24 |
|---|---|
| 자료구조 - 트리, 트리용어 (0) | 2022.11.23 |
| 스택 (0) | 2022.10.07 |
| 연결리스트 (0) | 2022.10.03 |
| 리스트와 노드 (0) | 2022.10.03 |




