| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- 인공지능
- opencv
- 코드구현
- 프로그래머스
- Convolution
- Self-supervised
- optimizer
- object detection
- 논문구현
- 파이토치
- 코딩테스트
- ViT
- cnn
- 머신러닝
- pytorch
- programmers
- Segmentation
- Python
- Ai
- transformer
- 딥러닝
- Computer Vision
- 옵티마이저
- 알고리즘
- 파이썬
- 논문
- 논문 리뷰
- 논문리뷰
- Semantic Segmentation
- Paper Review
- Today
- Total
Attention please
알고리즘 성능평가 본문
알고리즘의 성능 평가에 대해 설명하기 전에
프로그램이 무엇이고 알고리즘이 무엇인지에 대해 알아보겠습니다.
프로그램이란 알고리즘과 자료구조를 더하여 만드는 것입니다.
예를 들어 요리를 한다고 한다면
자료들은 요리를 위한 재료들이며,
알고리즘은 그 재료들을 손질하는 방법인 레시피입니다.
즉 알고리즘이란 문제를 해결하기 위한 단계적인 절차입니다.
그렇다면 어떤 알고리즘이 효율적인지 어떻게 알 수 있을까요?
알고리즘의 성능을 평가하기 위한 지표가 있습니다.
첫 번째로는 수행시간을 나타내는 시간복잡도와
두 번째로는 알고리즘이 수행되는 동안 사용되는 메모리 공간의 크기를 나타내는
공간 복잡도가 있습니다.
그중에서 저는 시간 복잡도에 대해 알아보겠습니다.
일반적으로 시간 복잡도가 공간 복잡도보다 더 중요합니다.
시간 복잡도란 입력데이터가 들어갔을 때 얼마나 시간이 걸리는 지를 알아보는 것입니다.
즉, 알고리즘(연산)이 실행되는 동안에 사용된
기본적인 연산 횟수를 입력 크기의 함수로 나타냅니다.
그중 점근표기법이라는 것이 있습니다.
시간복잡도를 근사치로 표현한 것입니다.
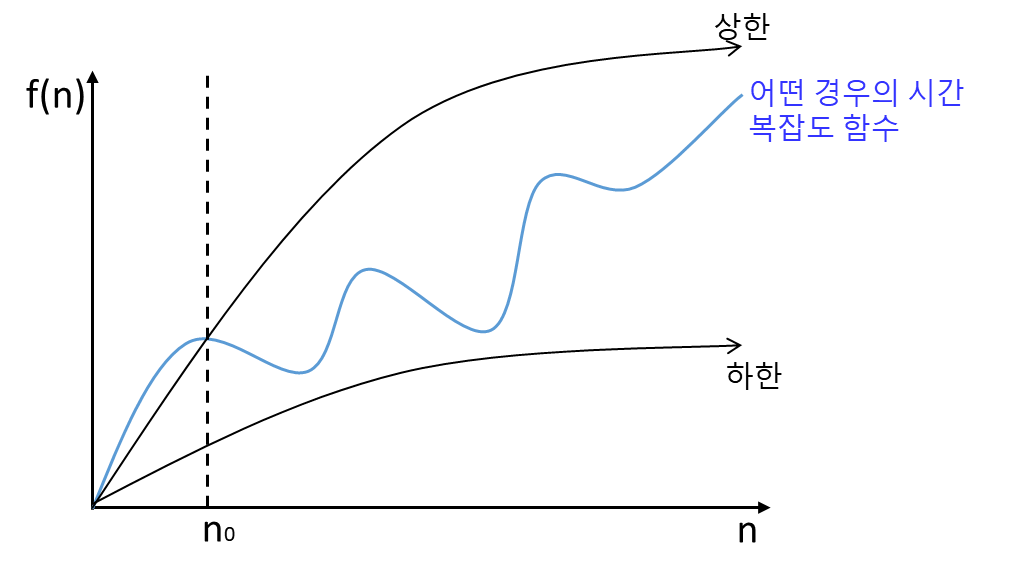
O - 표기법
O 표기의 정의란
모든 N ≥ N0에 대해서 f(N) ≤ cg(N)이 성립하는 양의 상수 c와N0이 존재하면,
f(N) = O(g(N))이다
입니다.
여기에서 저희들의 목표는 g(N)을 찾는 것이 됩니다.
위에서 말한 정의가 의미하는 두가지는
1. N0 이상의 모든 N에 대해서는 f(N)이 cg(N)보다 크지 않다는 의미이다.
2. g(N)을 f(N)의 상한이라는 의미이다.
이렇게 두가지정도의 의미를 가지고 있습니다.
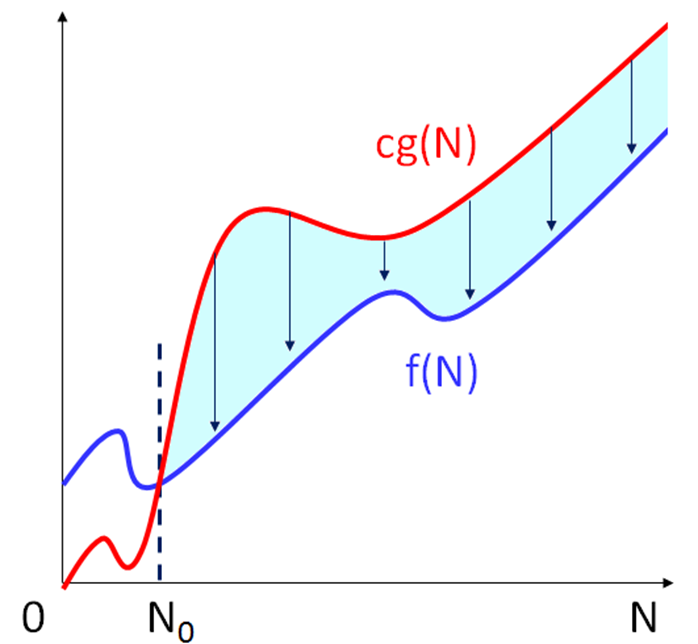
위는 O-표기법의 정의에 대해 시각적으로 표현한 것입니다.
O - 표기법 예시
$$\begin{align*} f(N)\;=\;2N^{2} + 3N + 5 \end{align*}$$
이러한 식이 존재할 때 구해야할 것은 g(N)입니다.
위에서 설명했던 것처럼 O-표기의 정의는
모든 N>N0 에 대해서,
f(N)<= cg(N)이 성립하는 양의 상수 c와 N0이 존재하면,
f(N) = O( g(N)) 이다.
였습니다.
즉 f(N)에서 최고차항의 계수가 2이므로 c를 2보다 큰 4로 정하고,
g(N)을 N^2로 정하게 되면
3보다 큰 모든 N에 대해
$$2N^{2}+3N+5\leq4N^{2}$$
이 성립하게 됩니다.
물론 g(N)은 N^2가 아닌 N^3도 가능합니다.
하지만 g(N)을 선택할 때는 정의를 만족하는 가장 차수가 낮은 함수를
선택하는 것이 바람직합니다.
$$f(N)\leq cg(N)$$
를 만족하는 가장 작은 c의 값을 찾지 않아도 됩니다.
그저 위의 식을 만족하는 양의 상수 c와 N0만 존재하면 된다.
그리하여 보통 O-표기를 찾기 위한 가장 간단한 방법은
다항식에서 최고차수의 항을 제외하고 나머지 항은 제거하여 g(N)을 정하는 것입니다.
$$2N^{2} + 3N + 5 \rightarrow N^{2}$$
Ω - 표기법(오메가)
Ω - 표기법에 대해 정의를 하자면
모든 N ≥ N0에 대해서 f(N) ≥ cg(N)이 성립하는 양의 상수 c와N0이 존재하면,
f(N) = Ω(g(N))이다
입니다.
위에서 설명드렸던 O-표기와는 반대입니다.
O-표기는 상한(upper bound)이지만
Ω - 표기는 하한(lower bound)입니다.
즉, O-표기를 이해하셨다면 이에 반대라고 생각하면 됩니다.
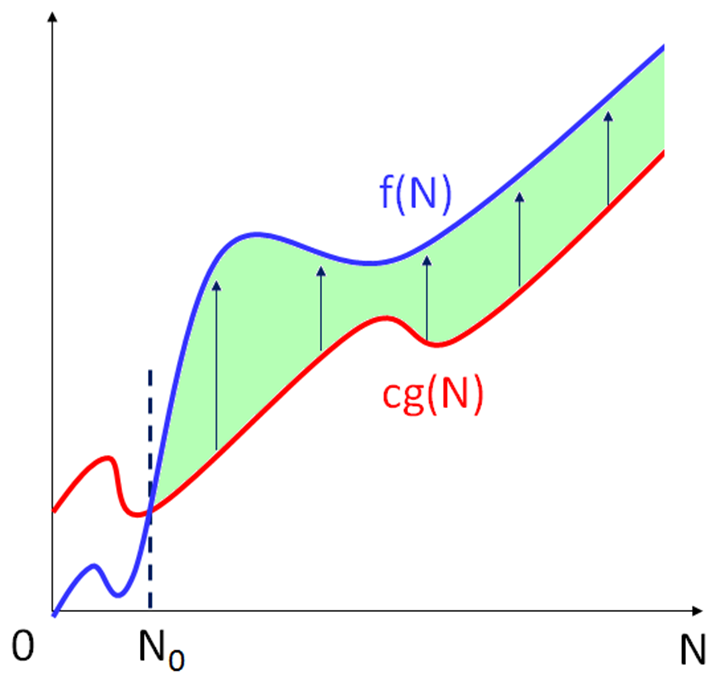
위 사진은 Ω - 표기를 시각화 한 것입니다.
O-표기와는 다르게 cg(N)이 f(N) 밑으로 내려온 것을 확인할 수 있습니다.
Θ (세타)-표기법
마지막으로 Θ에 대해 설명드리겠습니다.
Θ - 표기의 정의를 설명드리자면
모든 N ≥ N0에 대해서 c1g(N) ≥ f(N) ≥ c2g(N)이 성립하는 양의 상수 c1, c2, N0가 존재하면,
f(N) = Θ(g(N)) 이다.
로 설명될 수 있을 것 같습니다.
Θ - 표기는 o - 표기와 Ω - 표기가 동일한 경우에 사용합니다.
예를 들어,
$$\begin{align*} 2N^{2} + 3N + 5 = ?(N^{2}) \end{align*}$$
위 식은 ? 에 O 도 만족하고 Ω도 만족합니다.
이렇게 두 표기법 모두 동일한 경우에
Θ - 표기를 사용하는 것입니다.
즉
$$2N^{2} + 3N + 5 = ?(N^{3})$$
$$2N^{2} + 3N + 5 = ?(N)$$
의 경우에는 Ω-표기를 하지 않습니다.
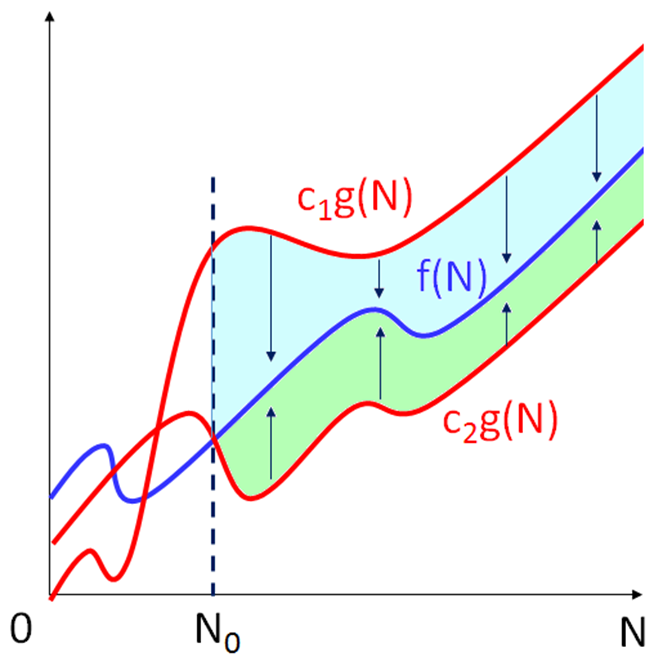
위 사진은 Ω - 표기를 시각적으로 표현한 것입니다.
상한가 하한가 모두 표시되는 것을 볼 수 있습니다.
이러한 경우에서
f(N) = Θ(g(N))
이 성립하게 됩니다.
O - 표기와 종류
알고리즘의 수행시간은 주로 O-표기를 사용합니다.
보다 정확히 표기하기 위해 Θ - 표기를 사용하기도 합니다.
위에서부터 아래로 내려갈 수록
비효율적인 알고리즘의 수행시간입니다.
O(1) : 상수시간
입력값이 아무리 커도 실행시간은 일정하다.
최적의 알고리즘 - 입력의 영향을 받지 않는다.
O(logN) : 로그(대수)시간
실행 시간은 입력값에 영향을 받긴 하지만, 웬만큼 큰 n에 대해서도 빠르다.
이진 검색 알고리즘 수행시간
값이 log를 취하면서 크기가 크게 줄어든다.
O(N) : 선형시간
입력값에 비례하여 수행시간이 증가한다.
O(NlogN) : 로그선형시간
대부분의 효율 좋은 정렬 알고리즘의 수행시간
(정렬 : 숫자 100개를 주고 정렬)
비교 기반 정렬 알고리즘은 로그선형시간보다 빠를 수 없다.
O(N^2) : 제곱시간
버블정렬과 같이
비효율적인 알고리즘의 수행시간이다.
O(N^3) : 세제곱시간
제곱시간에 비해 크기가 더 크다.
이 알고리즘까지는 버틸 수 있다.
O(2^N) : 지수시간
매우 비효율적인 알고리즘
지수시간부터 값이 기하급수적으로 나타나게 된다(2^N)
O(N!) : 계승시간
팩토리얼을 재귀적으로 계산하는 알고리즘 수행시간
아주 비효율적이며 n = 100만 되도 푸는 것이 거의 불가능하다.
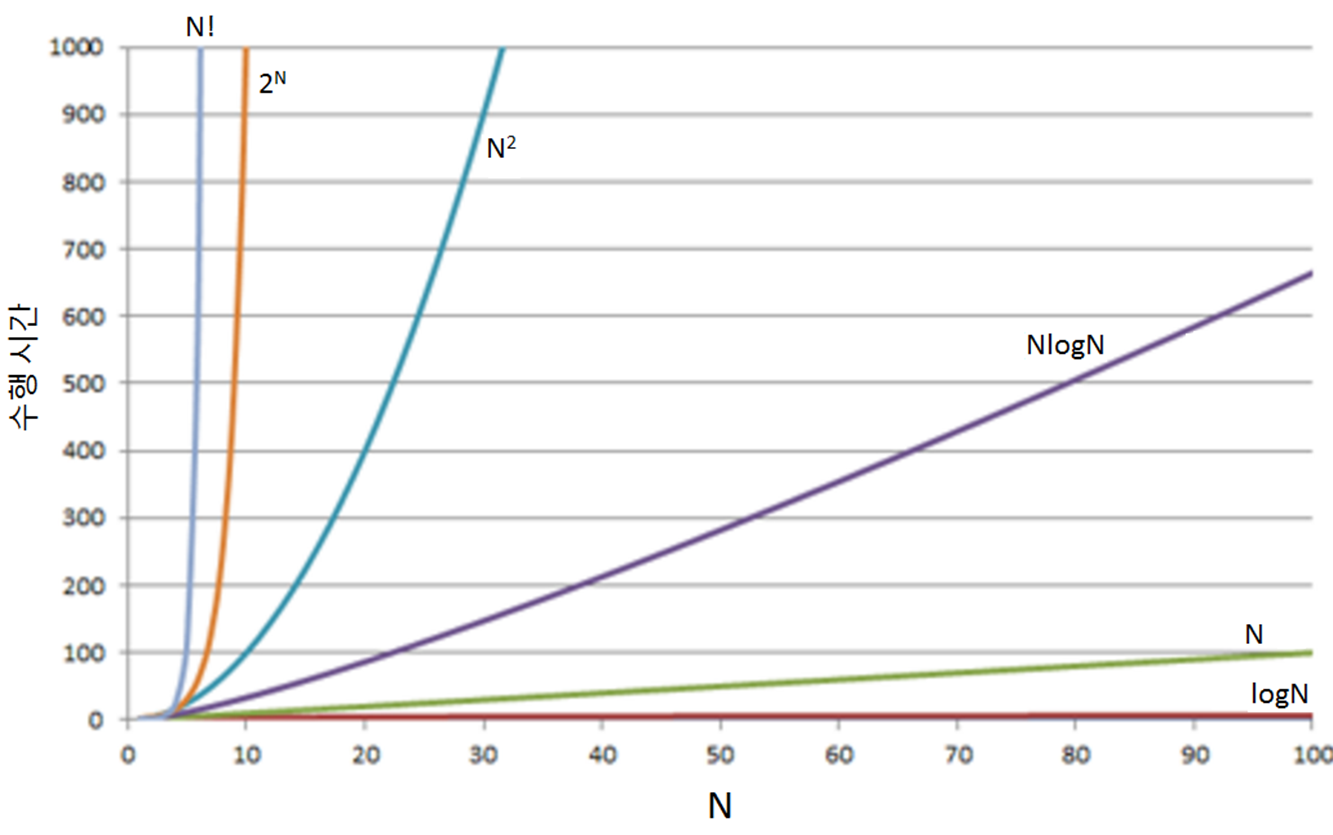
수행시간이 증가하면 증가할 수록
비효율적인 알고리즘입니다.
주의사항
O-표기와 최악의 경우를 가정하는 것은 같은 뜻이 아닙니다.
(최악의 경우는 입력값임)
빅오 표기법은 주어진 경우(최상/최악/평균)의 수행시간의 상한을 의미합니다.




