| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- Ai
- opencv
- 논문 리뷰
- Self-supervised
- Segmentation
- 머신러닝
- 파이토치
- transformer
- 코딩테스트
- Convolution
- 프로그래머스
- Computer Vision
- 인공지능
- optimizer
- 옵티마이저
- Paper Review
- Python
- 논문
- 파이썬
- Semantic Segmentation
- 코드구현
- ViT
- cnn
- 알고리즘
- object detection
- 논문구현
- 딥러닝
- 논문리뷰
- pytorch
- programmers
- Today
- Total
Attention please
[ISLR] 단순선형회귀 ; 잔차제곱합(residual sum of squares)을 최소화하자! 본문
단순선형회귀란?
통계학습을 위한 도구는 정말 다양합니다. 그 중에서도 단순선형회귀모형은 지도학습 방법 중 가장 간단하면서도 base가 되는 모형입니다. 이 기법은 하나의 설명변수 $ X $에 기초하여 양적 반응변수 $ Y $를 예측하죠.
단순선형회귀는 $ X $ 와 $ Y $ 사이에 선형적 상관관계가 있다고 가정합니다. 이때 선형적 상관관계가 무엇인지 간단하게 알아보도록 합시다.
$$ Y \approx \beta_{0} + \beta_{1}X $$
위 식은 수학적으로 선형적 상관관계를 나타낸 것이며, $ X $에 대한 $ Y $의 회귀라고 합니다. 만약 TV광고라는 변수를 통해 sales(판매량)을 추정하고 싶다면 $ sales \approx \beta_{0} + \beta_{1} \times TV $ 와 같이 sales와 TV 사이의 관계를 나타낼 수 있습니다.
이때 $ \beta_{0} $ 과 $ \beta_{1} $ 는 알려지지 않은 상수이며, 선형모델의 절편(intercept)과 기울기를 나타내며, 모델 계수 혹은 파라미터라고 불립니다. 만약 훈련 데이터를 통해 모델 계수에 대한 추정치 $ \hat{\beta_{0}} $, $ \hat{\beta_{1}} $ 을 구하면 특정 TV 광고 값을 기반으로 미래의 sales(판매량)을 다음과 같이 예측할 수 있게 됩니다.
$$ \hat{y} \approx \hat{\beta_{0}} + \hat{\beta_{1}}x $$
회귀계수 추정
회귀계수 $ \beta_{0}, \beta_{0} $ 은 실제 알려져 있는 계수가 아닌 추정해야할 계수입니다. 회귀계수를 추정하기 위해서는 $ X, Y $ 측정값으로 이루어져 있는 관측치가 필요하며 이를 훈련 데이터라고 부릅니다.
$$ (x_{1}, y_{1}), (x_{2}, y_{3}), ..., (x_{n}, y_{n}) $$
위와 같은 데이터 세트에 가장 가까운 직선, $ y_{i} \approx \hat{\beta_{0}} + \hat{\beta_{1}}x_{i} $ 가 되도록 하는 계수 추정값 $ \hat{\beta_{0}} $ 와 $ \hat{\beta_{1}} $ 를 얻는 것이 계수 추정의 목표입니다. 그렇다면 어떻게 훈련데이터를 얻을 수 있을까요?
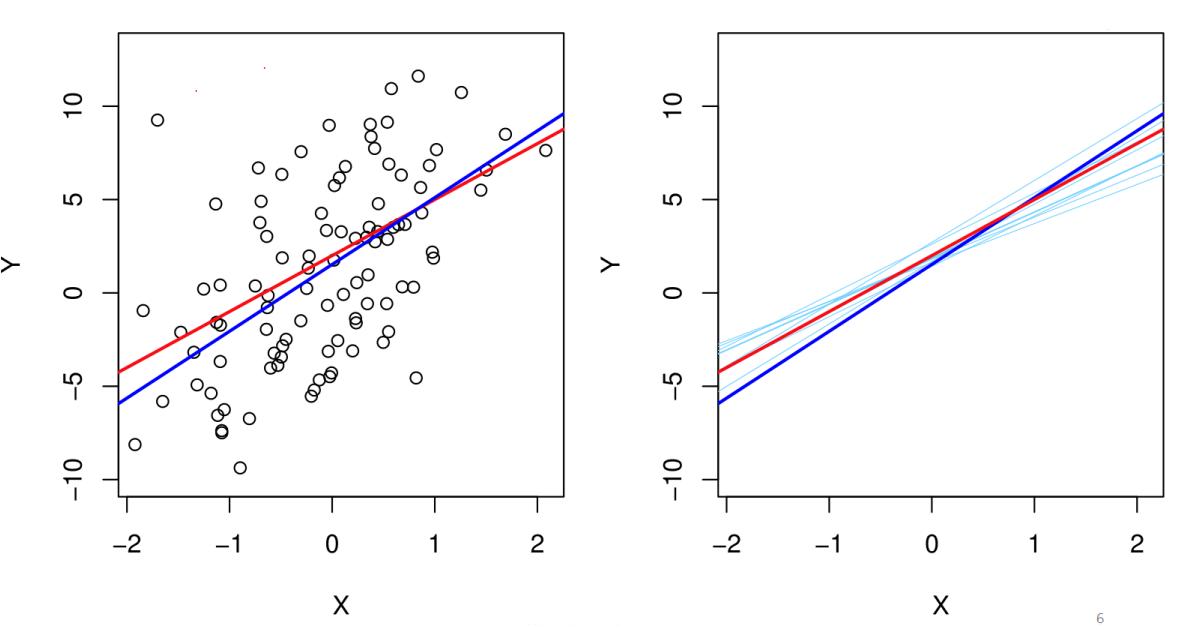
위 그림은 가상자료 $ f(x) = 2 + 3X $ 에 대해 실제 회귀직선과 LS(Least Squares)직선을 그린 것입니다. 즉, 계수 추정값 $ \hat{\beta_{0}} $ 와 $ \hat{\beta_{1}} $를 얻는 것은 실제 회귀직선을 얻는 것과 동일하므로 LS회귀직선이 True 회귀직선에 가까워야하며 다르게 말하면 두 직선간의 차이가 줄어들어야 합니다.
실제값과 예측값의 차이를 잔차(residual)이라 하며 식으로는 $ e_{i} = y_{i} - \hat{y_{i}} $ 이라 표현합니다. 이런 잔차는 양수와 음수로 이루어져있기 때문에 제곱하여 잔차의 크기를 유도할 수 있으며 잔차의 제곱을 모두 합한 값을 잔차제곱합(residual sum of squares; RSS) 라고 합니다.

즉, RSS를 minimize하는 것이 우리의 목표이기 때문에 위 식을 통해 RSS를 최소화하는 $ \hat{\beta_{0}} $ 와 $ \hat{\beta_{1}} $ 를 구할 수 있습니다.

최적화의 1계조건에 의해 편미분한 값이 0이 되는 식 $ a $와 $ b $를 얻었습니다. 이 식 2개를 연립하면 $ \hat{\beta_{0}} $ 와 $ \hat{\beta_{1}} $ 식을 유도할 수 있겠죠. 우선 식을 정리하면 다음과 같습니다.

추정해야할 계수 $ \hat{\beta_{0}} $ 와 $ \hat{\beta_{1}} $가 모두 각 식에 포함되어있습니다. 먼저 $ \hat{\beta_{1}} $를 구하기 위해 $ \hat{\beta_{0}} $이 있는 항을 소거하기 위해 $ a $식과 $ b $식에 적당한 값을 곱하여 연립해주겠습니다.

두 식을 연립하여 $ \hat{\beta_{1}} $ 에 대한 식이 만들어졌습니다. 구해야할 것은 $ \hat{\beta_{1}} $값이니 다시 식을 정리해줍시다.

유도된 $ \hat{\beta_{1}} $식을 바로 사용하기에는 아직 정리되지 않은 부분이 있습니다.


마지막으로 편차합에 맞는 폼으로 유도해주면 다음과 같습니다.

이때 $ S $ 를 편차합이라 하며 $ S_{xy} = \sum (x-\bar{x})(y-\bar{y}) $ 입니다. 결론적으로 $ \hat{\beta_{1}} $에 대한 식은 다음과 같습니다.

다음으로는 $ \hat{\beta_{0}} $에 대한 식을 유도해보도록 하죠. $ \hat{\beta_{0}} $은 $ \hat{\beta_{1}} $에 비해 유도과정이 간단합니다. 먼저 $ \hat{\beta_{1}} $ 유도과정 중에 사용했던 식 $ a $을 가져옵시다.

이미 $ \hat{\beta_{1}} $에 대한 식을 구했으니 $ \hat{\beta_{0}} $에 대한 식으로 유도해주기만 하면 됩니다.

정리하자면 $ \hat{\beta_{0}} $에 대한 식은 다음과 같습니다.

또한 편차합 $ S_{xx} $와 $ S_{xy} $ 에 대한 식을 유도하면 다음과 같습니다.

이를 통해 추정치 $ \beta_{0} $와 $ \beta_{1} $ 를 구한 후 독립변수가 주어졌을 때 추정값 $ \hat{y} $ 를 구할 수 있습니다.
'ISLR' 카테고리의 다른 글
| [ISLR] 통계학습(statistical learning)이란? (0) | 2023.05.05 |
|---|

