| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 논문
- Segmentation
- optimizer
- 강화학습
- 논문리뷰
- 옵티마이저
- opencv
- 논문구현
- ViT
- Semantic Segmentation
- transformer
- 파이썬
- 머신러닝
- 코드구현
- Python
- Computer Vision
- pytorch
- 인공지능
- 논문 리뷰
- 코딩테스트
- Self-supervised
- 파이토치
- Convolution
- programmers
- Ai
- 딥러닝
- cnn
- 프로그래머스
- object detection
- 알고리즘
- Today
- Total
Attention please
IoU(Intersection over Union)의 개념 및 코드 구현 본문
IoU란?
IoU란 Ground Truth와 모델이 예측한 값이 얼마나 겹쳐있는지 나타내는 Metric이다.
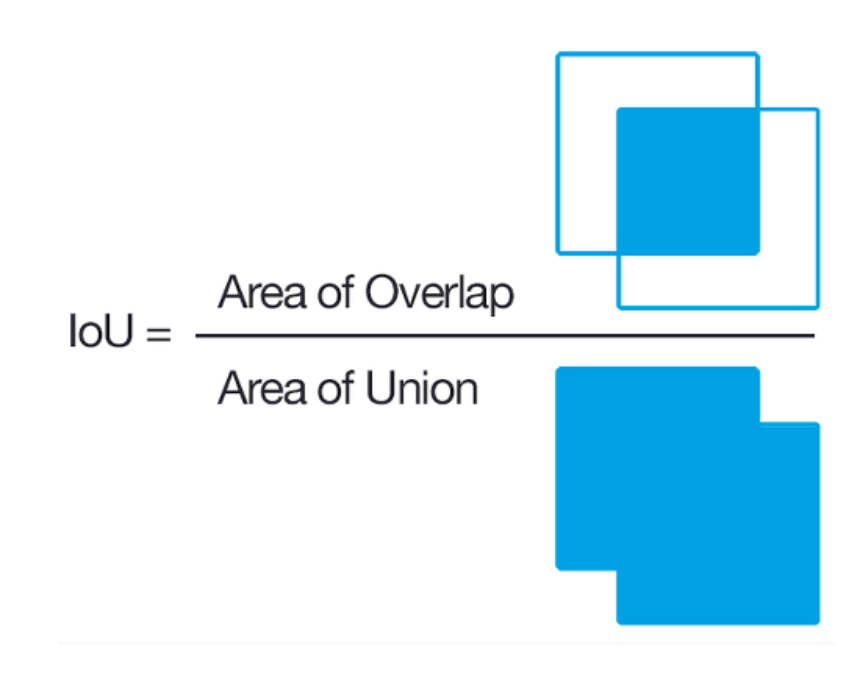
즉, IoU는 실제 box와 예측한 box의 교집합 / 합집합을 의미한다. 정답 영역과 예측 영역의 겹쳐진 부분이 크면 클수록 IoU값은 커진다. 물론 값이 크면 클수록 잘 예측했다고 판단한다.
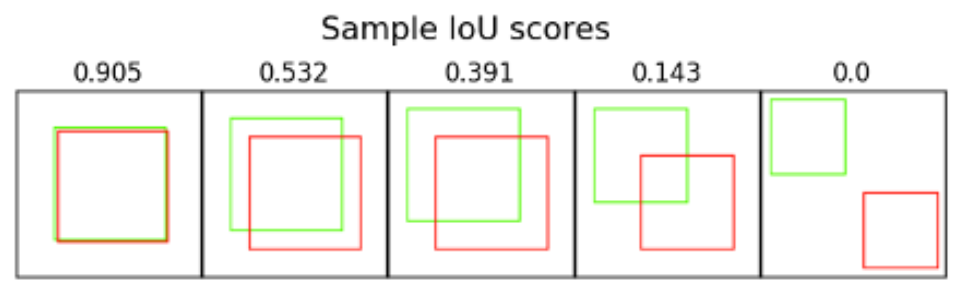
IoU의 최대값은 1이며, 최소값은 0이다.
IoU는 굉장히 엄격한 metric이기에 사람 눈으로 봤을 때는 object가 잘 검출된다고 느껴질지는 몰라도 IoU 값은 현저히 떨어질 수 있다.

고작 1/9 정도의 오차이기에 사람의 입장에서는 좋게 보여지지만 실제로 IoU값은 0.65 정도로 높지 않다. 그만큼 IoU Metric은 엄격한 평가지표임을 알 수 있다.
계산 방법
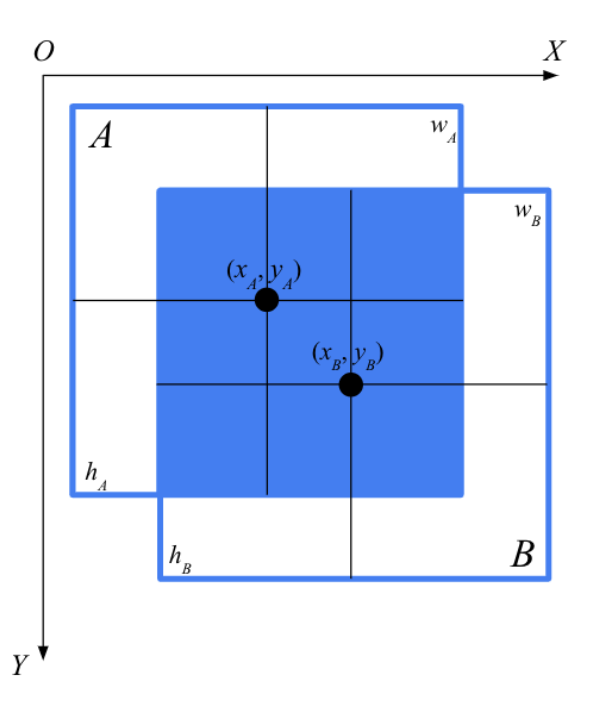
- x : 각 영역 중심의 x좌표
- y : 각 영역 중심의 y좌표
- h : 영역의 높이
- w : 영역의 너비
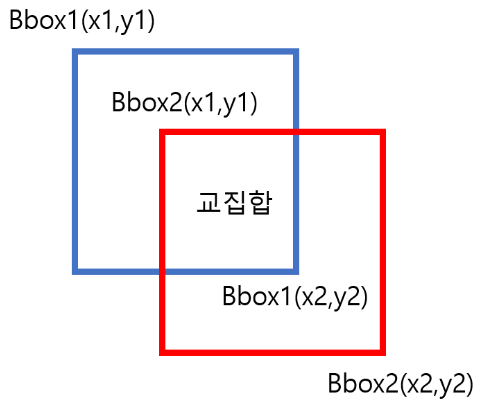
위 그림과 같이 2개의 영역이 주어지면 각 영역을 다음과 같이 표현할 수 있다.
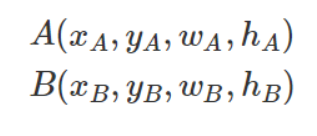
그 후에 dx 와 dy를 구한다.

위에서 구한 dx와 dy를 바탕으로 A영역과 B영역의 교집합과 합집합을 구한다.
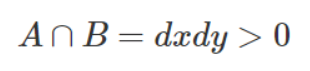

IoU는 교집합 / 합집합 이므로 위에서 구한 식을 바탕으로 IoU를 정의한다.
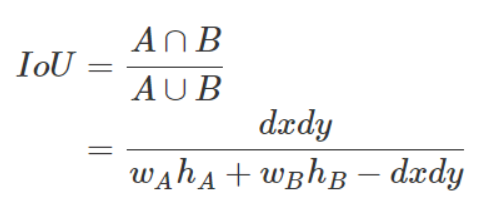
코드 구현
IoU를 코드로 구현하기 위해서는 bounding box에 대한 정보를 정의해야하는데 총 2가지 방법으로 정의할 수 있다.
(1) x1, y1, x2, y2
(x1, y1) 은 좌측 상단을 의미하는 좌표이며, (x2, y2) 는 우측 하단을 의미하는 좌표이다.
마치 드래그 하는 방식으로 정의한다고 생각하면 된다.
(2) x1, y1, w, h
(x1, y1)은 좌측 상단을 의미하는 좌표이며, w, h는 bounding box의 너비와 높이를 의미한다.
이번 IoU를 코드로 구현하기 위해 총 2개의 bounding box가 있다고 가정을 하고 정의하기 위한 방법으로는 (1) 방식으로 표현해보겠다.
다음과 같이 (1) 방법으로 2개의 bounding box를 정의하였고 다음으로 구해야 할 것은 교집합의 영역에 대한 좌표이다.
intersection_x1 = max(bbox1[0], bbox2[0])
intersection_y1 = max(bbox1[1], bbox2[1])
intersection_x2 = min(bbox1[2], bbox2[2])
intersection_y2 = min(bbox1[3], bbox2[3])
위에서 구한 교집합의 좌표를 이용해서 교집합을 구하자.
intersection = max(0, intersection_x2 - intersection_x1) * max(0, intersection_y2 - intersection_y1)
최종 코드는 다음과 같다.
def IoU(bbox1, bbox2):
# bounding box : [x1, y1, x2, y2]
# 교집합 구하기
intersection_x1 = max(bbox1[0], bbox2[0])
intersection_y1 = max(bbox1[1], bbox2[1])
intersection_x2 = min(bbox1[2], bbox2[2])
intersection_y2 = min(bbox1[3], bbox2[3])
intersection = max(0, intersection_x2 - intersection_x1) * max(0, intersection_y2 - intersection_y1)
# 각 box의 영역 구하기
box1_area = abs((bbox1[2] - bbox1[0]) * (bbox1[3] - bbox1[1]))
box2_area = abs((bbox2[2] - bbox2[0]) * (bbox2[3] - bbox2[1]))
# 합집합 : A + B - intersection(A,B)
return intersection / (box1_area + box2_area - intersection + 1e-7)
'딥러닝 > Computer Vision' 카테고리의 다른 글
| AP(Average Precision) & mAP(mean Average Precision)의 개념 (0) | 2022.12.30 |
|---|---|
| NMS(Non-maximum Suppression) 원리 (0) | 2022.12.30 |
| Separable & Depthwise & Pointwise Convolution 원리 및 Pytorch 구현 (0) | 2022.12.30 |
| Transposed Convolution 원리 및 Pytorch 구현 (0) | 2022.12.30 |
| Dilated Convolution(Atrous convolution) 원리 및 Pytorch 구현 (0) | 2022.12.30 |




