[논문 리뷰] DDQN: Deep Reinforcement Learning with Double Q-learning (2016)

이번에 리뷰할 논문은 Deep Reinforcement Learning with Double Q-learning 입니다.

https://arxiv.org/abs/1509.06461

Deep Reinforcement Learning with Double Q-learning

 

 

 

 

 

 

Problem Definition

$$Y_t^{\text{DQN}} \equiv R_{t+1} + \gamma \max_a Q(s_{t+1}, a \, ; \, \theta_t^-)$$

 

위 수식은 DQN에서 사용하는 TD target 입니다. 해당 식의 특징으로는 target sample을 뽑을 때, action에 대해서 가장 큰 $Q$값을 추출합니다. 하지만 본 논문에서는 해당 target sample을 뽑을 때 단순히 maximum값으로 추출하게 되면 overestimate 문제가 발생한다고 주장합니다. 

 

 

DQN에 대한 설명은 다음 글을 참고하시기 바랍니다.

2025.04.20 - [논문 리뷰/Reinforcement Learning] - [논문 리뷰] DQN: Playing Atari with Deep Reinforcement Learning (2013, 2015)

[논문 리뷰] DQN: Playing Atari with Deep Reinforcement Learning (2013, 2015)

 

 

우선 간단하게 overestimate가 되는 문제에 대해 설명하자면, 다음과 같이 모든 action에 대해 항상 같은 $Q$값이 나오는 optimal 한 상태를 가정합니다. 해당 state에서는 어떤 action을 취하더라도 항상 같은 $Q$값이 나오게 된다는 의미이고, 이를 $V_*(s)$ 라고 notation합니다. 

 

$$Q_*(s, a) = V_*(s)$$

 

이후, 기존의 DQN에서 $Q$를 업데이트하는 방식과 optimal $Q$에 대한 수식은 다음과 같이 나타나게 됩니다.

 

$$\max_a Q_t(s, a) \geq V_*(s) + \sqrt{\frac{c}{m - 1}}$$

 

즉, $max_a Q_t(s, a)$ 는 기존의 DQN의 업데이트 방식이며, $V_*(s)$ 는 실제로 다가가야 하는 optimal 한 최적의 가치 함수를 의미하죠. 

 

$$\max_a Q_t(s, a) - V_*(s) \geq \sqrt{\frac{c}{m - 1}}$$

 

위와 같이 수식을 정리하게 되었을 때, $Q$값을 max한 값으로 업데이트를 하게 되면 항상 optimal 한 값과의 차이가 발생, 즉, 항상 error가 발생한다는 것을 의미합니다. 본 논문에서는 이러한 점들을 기존 DQN의 문제로 정의하였고, 위와 같이 error가 발생함을 수학적으로 증명하였습니다. 

 

 

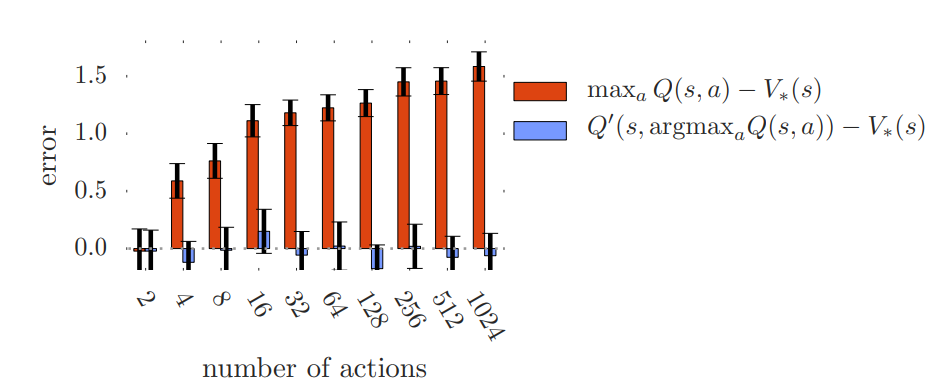
실제로 빨간색 bar는 기존 DQN의 방식으로 업데이트를 하였을 때의 optimal value와의 차이이고, 파란색 bar는 본 논문에서 제안한 방식으로 target sample을 추출하였을 때 optimal value와의 차이를 의미합니다. 위 그림과 같이 본 논문에서 제안한 방식으로 sampling을 하였을 때, error가 현저하게 떨어지는 것을 확인할 수 있습니다. 

 

위 그래프를 보시면, action 수가 많아질수록 error 수치가 점점 커지는 것을 확인할 수 있습니다. 그 이유는 만약 기존 DQN의 방식대로 모든 action에 대해서 가장 큰 $Q$값을 가지는 target sample을 추출하게 되면, 다른 action들이 다채롭게 존재하지만 이를 무시하고, 가장 큰 Q값을 가지는 action에 대해서만 과도하게 평가, 즉, overestimate 될 수 있습니다. 이러한 이유로 action 수가 많아질수록 overestimate 의 문제가 더 커지게 되고 위와 같이 error 수치도 증가하게 되는 것이죠.

 

 

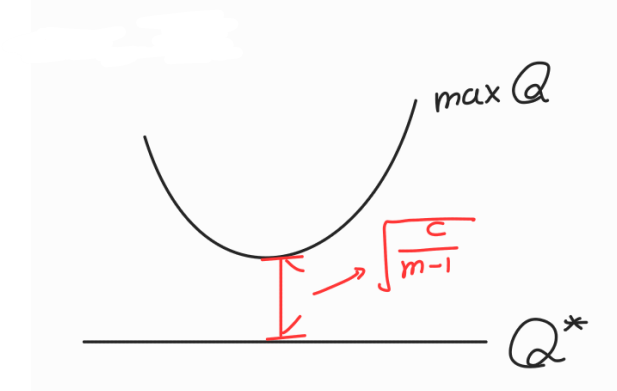
즉, 위 그림과 같이 $\text{max} Q$ 와 optimal $Q_*$ 사이에는 $\sqrt{\frac{c}{m - 1}}$만큼의 차이가 발생한다는 것을 본 논문에서 밝히게 됩니다. 

 

 

 

 

 

 

Target Value

우선 본 논문에서 제안하는 target 수식은 다음과 같습니다.

 

$$R_t + \gamma Q_{w^-}\left(s_{t+1}, \arg\max_{a_{t+1}} Q_{w}(s_{t+1}, a_{t+1})\right)$$

 

• $w$ : main network의 파라미터
• $w^-$ : target network의 파라미터

원래 DQN의 target 수식은 $R_t + \gamma \max_{a_{t+1}} Q_{w^-}(s_{t+1}, a_{t+1})$ 입니다. target을 구할 때 target network를 따로 분리하여 샘플링을 하였지만 여전히 target network로부터의 Q값을 기준으로 maximum값을 사용했기 때문에 overestimate가 존재했죠. 다시 말해, 기존 DQN은 max연산을 Q값에 직접 적용하였으며, 이는 Q가 과하게 큰 액션이 반복적으로 선택하도록 하였습니다.

 

하지만 DDQN에서는 선택은 main network, 평가는 target network 로 하여 분리된 신경망으로 명확하게 역할을 분담시켰습니다. 이를 통해 더 안정적인 업데이트를 이끌어냈다고 볼 수 있습니다.

 

 

 

 

 

 

Proof Theorem

증명해야 하는 theorem 수식은 다음과 같습니다.

 

$$\text{Theorem:} \quad \max_a Q_t(s, a) \geq V_*(s) + \sqrt{\frac{c}{m - 1}}$$

 

우선 위 수식을 증명하기 위해 다음 3가지의 가정이 필요합니다.

 

1. 모든 액션에 대해 $Q^*$ 값이 동일

$$\text{Given } s_t, \quad Q^*(s_t, a_t) = V^*(s_t) \quad \forall a_t$$

이는 말 그대로 어떠 상태 $s_t$에서 모든 action에 대해 $Q$값이 전부 같다는 의미입니다. 즉, 에이전트가 어떤 행동을 하든 그 상태에서는 기대되는 보상이 똑같습니다.

 

 

2. 평균 오차는 0

$$\sum_a \varepsilon_a = 0, \quad \text{where } \varepsilon_a \triangleq Q(s_t, a_t) - V^*(s_t)$$

여기서 $\varepsilon_a$는 추정된 Q값과 실제 최적값의 차이를 의미합니다. 이 차이값들의 평균이 0이라는 의미는 Q함수가 편향은 없고 단순히 샘플링 노이즈만 있다는 가정으로 볼 수 있습니다.

 

 

3. 분산은 $\frac{1}{m} \sum_a \varepsilon_a^2 = C \quad \text{where } C > 0$

$$\frac{1}{m} \sum_a \varepsilon_a^2 = C \quad \text{where } C > 0,\ m = \text{num of actions}$$

Action 수 $m$개의 오차 제곱 평균이 일정한 값 $C$라는 뜻입니다. 즉, 각 action에 대한 Q값의 오차가 고르게 퍼져 있고, 그 강도는 C로 일정하다는 것을 의미합니다. 

 

---

 

자 이제 위에서 주어진 3가지 조건을 두고 다음 수식을 증명해야 합니다.

 

$$\max_a \varepsilon_a \geq \sqrt{\frac{C}{m - 1}}$$

 

위 수식에서 $\varepsilon$은 $Q(s_t, a_t) - V^*(s_t)$ 입니다. 하지만 $V^*(s_t)$ 에는 action이 파라미터로 없기 때문에 결론적으로는 다음과 같은 수식임을 증명하는 것이 됩니다.

 

$$\max_a Q(s, a) - V^*(s) \geq \sqrt{\frac{C}{m - 1}}$$

 

이를 증명하기 위해 다음과 같이 notation을 하겠습니다.

 

• $n$ : 양수 action의 개수 ($\varepsilon_a$ > 0)
• $m-n$ : 음수 action의 개수 ($\varepsilon_a$ < 0)

우선 2번 조건인 $\sum_a \varepsilon_a = 0$을 만족시키기 위해서는 $n$ 혹은 $m-n$이 0인 것은 불가능합니다. 즉, 모두 음수이거나 양수인 것은 불가능하죠. 

 

또한 3번 조건인 $\frac{1}{m} \sum_a \varepsilon_a^2 = C$을 만족하기 위해서는 $\varepsilon_a$가 모두 0인 것도 불가능합니다. 그리고 반드시 $m-n \geq 1$ 이어야 합니다.

 

또한 다음 수식도 만족합니다.

 

$$\sum_a \varepsilon_a^+ \leq n \max_a \varepsilon_a$$

• $\varepsilon_a^+$ : 양수인 $\varepsilon_a$
• $\varepsilon_a^-$ : 음수인 $\varepsilon_a$

이후 다음과 같이 가정을 하나 해봅니다.

 

$$n \max_a \varepsilon_a < n \sqrt{\frac{c}{m - 1}}$$

$$\max_a \varepsilon_a < \sqrt{\frac{c}{m - 1}}$$

 

위 가정을 증명해볼건데 결론부터 말씀드리면 위 가정은 만족하지 않습니다. 그러면서 자연스럽게 $\max_a \varepsilon_a \geq \sqrt{\frac{c}{m - 1}}$ 가 만족하면서 theorem을 증명하게 됩니다.

 

다음으로 위 가정을 만족한다면, $\sum_a \varepsilon_a^+ \leq n \max_a \varepsilon_a < n \sqrt{\frac{c}{m - 1}}$ 와 같이 나타낼 수 있으며, $\sum_a \varepsilon_a = 0$ 을 만족해야하므로 다음과 같습니다.

 

$$\sum_a |\varepsilon_a^-| < n \sqrt{\frac{c}{m - 1}}$$

 

또한 위 수식을 만족한다면, 다음과 같이 나타낼 수 있습니다.

 

$$\max_a |\varepsilon_a^-| < n \sqrt{\frac{c}{m - 1}}$$

 

 

 

다음 수식을 보면,

 

$$\sum_a |\varepsilon_a^-|^2 \leq \sum_a |\varepsilon_a^-| \cdot \max_a |\varepsilon_a^-|$$

 

위 수식이 만족하는 이유는 간단합니다. 예를 들어서 $\varepsilon_a^-$ 가 -1, -2, -3 이 있다고 한다면, 각 수에 대해 절대값을 취하고, 각각 최대값과 곱하는 것이 당연히 각 값의 제곱보다 클 수 밖에 없습니다. 

 

$$1^2 + 2^2 + 3^2 \leq (1 \cdot 3) + (2 \cdot 3) + (3 \cdot 3)$$

 

앞서 정의하였던 두 가정 ( $\sum_a |\varepsilon_a^-| < n \sqrt{\frac{c}{m - 1}}$ ) 과 ( $\max_a |\varepsilon_a^-| < n \sqrt{\frac{c}{m - 1}}$ ) 이 만족한다면, 다음과 같이 수식을 전개해나갈 수 있습니다.

 

$$\sum_a \left| \epsilon_a^- \right|^2  \leq \sum_a \left| \epsilon_a^- \right| \cdot \max_a \left| \epsilon_a^- \right|$$
$$\sum_a \left| \epsilon_a^- \right|^2 < n \sqrt{ \frac{c}{m - 1} } \cdot n \sqrt{ \frac{c}{m - 1} } = \frac{n^2 c}{m - 1}$$

 

또한 $m-n \geq 1$ 이므로 $m-1 \geq n$ 으로 나타낼 수 있기 때문에 다음과 같이 전개가 가능합니다. 

 

$$\frac{n^2 c}{m - 1} \leq (m-1) \cdot c$$

 

 

다음으로 $\sum_{a} \varepsilon_a^+ \leq n \max_a \varepsilon_a < n \sqrt{\frac{c}{m-1}}$ 이 수식이 만족한다고 가정하였었는데, 해당 수식에 각 항에 제곱을 해주면 다음과 같이 나타낼 수 있습니다. 

 

$$\sum_{a} (\varepsilon_a^+)^2 < n \cdot \frac{c}{m-1}$$

 

또한 앞서 전개하였던 $\sum_a \left| \epsilon_a^- \right|^2 \leq \sum_a \left| \epsilon_a^- \right| \cdot \max_a \left| \epsilon_a^- \right|$ 수식에 $(\varepsilon_a^+)^2$의 합을 더해주게 되면 다음과 같이 전개가 가능합니다.

 

$$\sum_a  \varepsilon_a^2  \leq  \underbrace{     \sum_a \left| \varepsilon_a^- \right| \cdot \max_a \left| \varepsilon_a^- \right| }_{\text{음수 } \varepsilon \text{ 제곱의 합}}  +  \underbrace{     \sum_a \left( \varepsilon_a^+ \right)^2 }_{\text{양수 } \varepsilon \text{ 제곱의 합}}$$

 

$$\sum_a  \varepsilon_a^2 < n \sqrt{ \frac{c}{m - 1} } \cdot n \sqrt{ \frac{c}{m - 1} } + n \frac{c}{m-1}$$

 

$$\sum_a  \varepsilon_a^2 < \frac{n^2 c}{m-1} + n \frac{c}{m-1}$$

 

여기서 $m-1 \geq n$ 이므로 다음과 같이 전개됩니다.

 

$$\sum_a  \varepsilon_a^2 < (m-1) \cdot c + (m-1) \frac{c}{m-1}$$

 

$$\sum_a \varepsilon_a^2 < mc$$

 

근데, 앞서 정의하였던 3번 조건인 ($\frac{1}{m} \sum_a \varepsilon_a^2 = C \rightarrow \sum_a \varepsilon_a^2 = mC$) 을 만족하지 못합니다. 고로 모순이 생겼다는 것을 의미합니다. 

 

해당 모순은 $\max_a \varepsilon_a < \sqrt{\frac{c}{m - 1}}$ 에서 시작하였기 때문에, 결론적으로는 다음 수식을 만족하게 되는 것입니다. 

 

$$\max_a \varepsilon_a \geq \sqrt{\frac{c}{m - 1}}$$

 

 

 

 

 

 

Result

위 증명하는 과정을 통해 $\max_a \varepsilon_a \geq \sqrt{\frac{c}{m - 1}}$ 이 만족함을 알 수 있었습니다. 즉, 기존의 DQN 방식의 업데이트로는 항상 error가 발생한다는 것을 의미합니다. 

 

본 논문에서는 TD target을 샘플링하는 새로운 방식을 소개하며, 이는 $\max_a \varepsilon_a \geq \sqrt{\frac{c}{m - 1}}$ 를 만족하지 않아 더 최적화하는 데 알맞다고 합니다.

 

$$R_t + \gamma Q_{w^-}\left(s_{t+1}, \arg\max_{a_{t+1}} Q_{w}(s_{t+1}, a_{t+1})\right)$$

 

위 식에서는 target을 maximum으로 잡지 않기 때문이죠.