| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- transformer
- Segmentation
- 논문리뷰
- 강화학습
- pytorch
- Convolution
- ViT
- 알고리즘
- programmers
- object detection
- 논문 리뷰
- Self-supervised
- 머신러닝
- 파이썬
- Semantic Segmentation
- 인공지능
- 파이토치
- 프로그래머스
- 논문구현
- Computer Vision
- optimizer
- opencv
- cnn
- 코드구현
- 논문
- 딥러닝
- Ai
- 코딩테스트
- 옵티마이저
- Python
- Today
- Total
Attention please
[강화 학습] Q-learning 완전 정복 본문
Q-learning
앞서 다루었던 TD(Temporal Difference) 에서 target policy와 behavior policy가 동일한 경우 on-policy, 동일하지 않은 경우 off-policy라고 하였습니다. 그 중, 이번에 다룰 Q-learning은 off-policy 알고리즘입니다.
2025.04.15 - [딥러닝/Reinforcement Learning] - [강화 학습] On-policy vs Off-policy
[강화 학습] On-policy vs Off-policy
Temporal DifferenceOn-policy 와 Off-policy에 대해 들어가기 전 TD(Temporal Difference)에 대해 다시 한번 짚고 넘어가보도록 하겠습니다. $$Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha \left( R_t + \gamma Q(s_{t+1}, a_{t+1}) - Q(s_t,
smcho1201.tistory.com
우선, 각 target policy와 behavior policy를 정의하여야 합니다.
$$ \text{target policy: } P(a_{t+1} \mid s_{t+1}) = \delta(a_{t+1} - a^*_{t+1}), \quad a^*_{t+1} = \arg\max_{a_{t+1}} Q(s_{t+1}, a_{t+1})$$
$$\text{behavior policy: } \epsilon\text{-greedy}$$
Target policy의 경우, 위 수식과 같이 정의됩니다. 여기서 나오는 $\delta$함수는 Dirac delta function을 의미하는데, 쉽게 말해 $a_{t+1}$은 항상 $a^*_{t+1}$만 선택한다는 의미입니다. 근데 보시다시피 $a^*_{t+1}$는 $ \arg\max_{a_{t+1}} Q(s_{t+1}, a_{t+1}) $ 라고 하였고, 이는 항상 $Q$ 값이 최대가 되도록 하는 $a_{t+1}$을 선택한다는 의미입니다. 즉, greedy하게 선택을 한다는 의미이죠.
Behavior policy의 경우, $ \epsilon\text{-greedy} $ 라 되어있습니다. Target policy와는 다르게 행동을 고를 때는 $\epsilon$ 확률로 탐험을 포함하는 것을 의미합니다. 즉, 데이터는 $ \epsilon\text{-greedy} $ 로 수집되는 것이죠.
그러면 각 policy에 대한 정의를 모두 끝냈으니, Q-learning의 Bellman 기대식을 전개해봅시다. 원래 식은 다음과 같이 Bellman 부등식에 의해 전개가 됩니다.
$$Q(s_t, a_t) = \int \left( R_t + \gamma Q(s_{t+1}, a_{t+1}) \right)
\cdot P(a_{t+1} \mid s_{t+1})
\cdot P(s_{t+1} \mid s_t, a_t) \, da_{t+1} \, ds_{t+1}
$$
여기서, $ P(a_{t+1} \mid s_{t+1}) $ 는 target policy 이고, $ P(s_{t+1} \mid s_t, a_t) $는 behavior policy인 $ P(a_t \mid s_t)$ 로부터 나온 transition이라고 하였습니다. 근데, Q-learning은 target policy가 $ \delta(a_{t+1} - a^*_{t+1}) $라고 하였으므로 다음과 같이 전개할 수 있습니다.
$$= \int_{s_{t+1}, a_{t+1}} \left( R_t + \gamma Q(s_{t+1}, a_{t+1}) \right)
\cdot \delta(a_{t+1} - a^*_{t+1})
\cdot P(s_{t+1} \mid s_t, a_t) \, da_{t+1} \, ds_{t+1}
$$
위 식에서 결국 $ \delta(a_{t+1} - a^*_{t+1}) $ 가 의미하는 바는 $ Q(s_{t+1}, a_{t+1}) $ 의 $a_{t+1}$ 에 항상 $a^*_{t+1}$을 대입하라는 것과 동일합니다. 최종적으로 $a_{t+1}$는 적분에서 빠져나와 다음과 같이 전개가 됩니다.
$$ Q(s_t, a_t) = \int_{s_{t+1}} \left( R_t + \gamma Q(s_{t+1}, a^*_{t+1}) \right)
\cdot P(s_{t+1} \mid s_t, a_t) \, ds_{t+1}
$$
$$= \int_{s_{t+1}} \left( R_t + \gamma \max_{a_{t+1}} Q(s_{t+1}, a_{t+1}) \right)
\cdot P(s_{t+1} \mid s_t, a_t) \, ds_{t+1}
$$
위 수식을 보면, Q-learning에서 TD-target은 $R_t + \gamma \max_{a_{t+1}} Q(s_{t+1}, a_{t+1})$임을 알 수 있습니다.
n-step TD & n-step Q-learning
앞서 TD의 경우 $t+1$에 대한 기댓값입니다. 즉, 1-step TD에서의 기댓값이라 볼 수 있죠.
$$Q(s_t, a_t) = \int_{s_{t+1}, a_{t+1}} \left( R_t + \gamma Q(s_{t+1}, a_{t+1}) \right)
\cdot P(a_{t+1} \mid s_{t+1}) \cdot P(s_{t+1} \mid s_t, a_t) \, da_{t+1} \, ds_{t+1}$$
위 수식을 보면, 다음 상태인 $s_{t+1}$와 그에 따른 행동 $a_{t+1}$에 대한 기대 보상을 $Q$로 추정합니다. 여기서 $t+2$만큼 더 나아가면, 다음 수식과 같이 2-step TD 방식으로 나타낼 수 있습니다.
$$= \int_{s_{t+1}, a_{t+1}, s_{t+2}, a_{t+2}} \left( R_t + \gamma R_{t+1} + \gamma^2 Q(s_{t+2}, a_{t+2}) \right)
\cdot P(a_{t+2} \mid s_{t+2}) \cdot P(s_{t+2} \mid s_{t+1}, a_{t+1})
\cdot P(a_{t+1} \mid s_{t+1}) \cdot P(s_{t+1} \mid s_t, a_t)
\, da_{t+2} \, ds_{t+2} \, da_{t+1} \, ds_{t+1}$$
위 수식에서 $P(a_{t+2} \mid s_{t+2})$ 은 target policy이며, $Q(s_{t+2}, a_{s+2})$를 샘플링하는데 필요한 정책입니다. 하지만, $ P(s_{t+2} \mid s_{t+1}, a_{t+1}) $ 와 $ P(s_{t+1} \mid s_t, a_t) $는 각각 behavior policy인 $q(a_{t+1} \mid s_{t+1})$와 $q(a_t \mid s_t) $로부터 정해지는 state입니다. (여기서 target policy와 behavior policy를 구분하기 위해 각각 $P$ 와 $q$로 구분하도록 하겠습니다.)
다시 말해 수식을 보면, $ P(a_{t+1} \mid s_{t+1}) $ 에서 샘플링을 하고자 하지만, 1-step TD와 달리 2-step에 대한 target을 샘플링해야 하기 때문에, $q(a_{t+1} \mid s_{t+1})$ 에서 뽑아야 합니다. 이를 위해 importance sampling 을 사용합니다.
Importance sampling
원래의 일반적인 기댓값 계산은 다음과 같습니다.
$$\int_x x P(x) \, dx \approx \frac{1}{N} \sum_{i=1}^{N} x_i, \quad x_i \sim P(x)$$
만약 위 식과 같이 $P$에서 직접 샘플링이 가능하다면 간단하게 평균값을 취해 추정이 가능하지만, 앞서 2-step TD와 같이 $P$가 아닌 $q$로부터 샘플링을 해야하는 상황과 같이 현실에서는 $P$에서 직접 샘플링이 어려운 경우가 많습니다. 그래서 더 쉽게 샘플링이 가능한 $Q(x)$로부터 뽑되, 샘플의 중요도를 보정해주는 방식이 바로 Importance sampling 입니다.
$$= \int_x \frac{P(x)}{Q(x)} \cdot x Q(x) \, dx
\approx \frac{1}{N} \sum_{i=1}^{N} x_i \cdot \frac{P(x_i)}{Q(x_i)}, \quad x_i \sim Q(x)
$$
위 수식을 보면, $x_i$를 더 샘플링하기 쉬운 $Q(x)$ 분포에서 뽑지만, 원래 분포와의 차이를 $ \frac{P(x_i)}{Q(x_i)} $ 가중치로 보정해주는 식입니다. 이렇게 하면 마치 $P$에서 뽑은 것처럼 기댓값을 계산할 수 있게 되는 것이죠.
TD Target
앞서 2-step TD은 다음과 같이 전개되었습니다.
$$Q(s_t, a_t) = \int_{s_{t+1}, a_{t+1}, s_{t+2}, a_{t+2}} \left( R_t + \gamma R_{t+1} + \gamma^2 Q(s_{t+2}, a_{t+2}) \right)
\cdot P(a_{t+2} \mid s_{t+2}) \cdot P(s_{t+2} \mid s_{t+1}, a_{t+1})
\cdot P(a_{t+1} \mid s_{t+1}) \cdot P(s_{t+1} \mid s_t, a_t) \, da_{t+2} \, ds_{t+2} \, da_{t+1} \, ds_{t+1}
$$
하지만 behavior policy인 $q$로부터 샘플링을 하기 위해 Importance sampling을 사용하여야 하며, 결과적으로 다음과 같이 전개됩니다.
$$ Q(s_t, a_t) = \int_{s_{t+1}, a_{t+1}, s_{t+2}, a_{t+2}} \left( R_t + \gamma R_{t+1} + \gamma^2 Q(s_{t+2}, a_{t+2}) \right)
\cdot P(a_{t+2} \mid s_{t+2}) \cdot P(s_{t+2} \mid s_{t+1}, a_{t+1})
\cdot \frac{P(a_{t+1} \mid s_{t+1})}{q(a_{t+1} \mid s_{t+1})}
\cdot P(s_{t+1} \mid s_t, a_t) \cdot q(a_{t+1} \mid s_{t+1}) \, da_{t+2} \, ds_{t+2} \, da_{t+1} \, ds_{t+1}
$$
여기서 target policy인 $ P(a_{t+2} \mid s_{t+2}) $는 $Q$값이 최대가 되도록 greedy하게 sampling하는 것이며, $\delta (a_{t+2} - a^*_{t+2})$ 로 나타낼 수 있습니다. ($Q$값이 max가 되도록 하는 $a^*_{t+2}$만 sampling)
그러면 최종적으로 TD target은 다음과 같이 나타낼 수 있습니다.
$$\text{TD target} = \frac{P(a_{t+1}^{(N)} \mid s_{t+1}^{(N)})}{q(a_{t+1}^{(N)} \mid s_{t+1}^{(N)})}
\cdot \left( R_t + \gamma R_{t+1} + \gamma^2 \max_{a_{t+2}} Q(s_{t+2}^{(N)}, a_{t+2}^*) \right)
$$
하지만 일반적으로 TD target을 샘플링할 때, $ \frac{P(a_{t+1}^{(N)} \mid s_{t+1}^{(N)})}{q(a_{t+1}^{(N)} \mid s_{t+1}^{(N)})} $는 계산에서 제외된다고 합니다. 그 이유는 다음 그림을 보면,
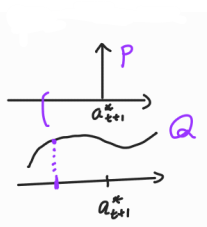
Target policy인 $P$는 항상 $a^*_{t+1}$만을 greedy하게 샘플링을 하며, Behavior policy인 $q$는 $\epsilon \text{-greedy}$하게 샘플링을 하죠. 하지만 $\frac{P}{q}$와 같이 나누어지게 되면, $a^*_{t+1}$ 가 아닌 경우에 값은 항상 0이게 됩니다.(확률밀도함수, pdf에서 범위가 아닌 $a^*_{t+1}$을 뽑을 확률은 항상 0) 즉, 보정으로서 곱해지는 $\frac{P}{q}$ 의 의미가 없어지게 되기 때문에 그냥 생략 후 샘플링을 진행한다고 합니다.
그래서 최종적으로 2-step Q-learning의 target은 다음과 같습니다.
$$\text{TD target} = \left( R_t + \gamma R_{t+1} + \gamma^2 \max_{a_{t+2}} Q(s_{t+2}^{(N)}, a_{t+2}^*) \right)
$$
'딥러닝 > Reinforcement Learning' 카테고리의 다른 글
| [강화 학습] On-policy vs Off-policy (1) | 2025.04.15 |
|---|---|
| [강화 학습] Monte Carlo(MC) & Temporal Difference(TD) (2) | 2025.04.14 |
| [강화 학습] 가치 함수(Value Function) 및 벨만 방정식(Bellman Equation) 정의 및 증명 (1) | 2025.04.13 |



